Authors: Hiroyuki Kasai
Last page update: July 22, 2022
Latest library version: 2.1 (see Release notes for more info)
We are very welcome to your contribution. Please tell us
- NMF solvers written by MATLAB,
- appplication MATLAB flies using NMF solvers, and
- your comments and suggestions.
The NMFLibrary is a pure-Matlab library of a collection of algorithms of non-negative matrix factorization (NMF). The solvers can be also called from python (see demo.py).
If this library is useful for you, please cite this as presented below:
@misc{kasai_NMFLibrary_2017,
Author = {Kasai, Hiroyuki},
Title = {{NMFLibrary}: MATLAB library for non-negative matrix factorization (NMF)},
Year = {2017},
Howpublished = {\url{https://github.com/hiroyuki-kasai/NMFLibrary}}
}
-
Frobenius-norm
-
Fro-MU (multiplicative updates)
- MU
- D.D. Lee and H. S. Seung, "Algorithms for non-negative matrix factorization," NIPS, 2000. (for Euclidean distance and Kullback-Leibler divergence (KL))
- A.Cichocki, S.Amari, R.Zdunek, R.Kompass, G.Hori, and Z.He, "Extended SMART algorithms for non-negative matrix factorization," Artificial Intelligence and Soft Computing, 2006. (for alpha divergence and beta divergence)
- Modified MU
- C.-J. Lin, "On the convergence of multiplicative update algorithms for nonnegative matrix factorization," IEEE Transactions on Neural Network, vol.18, no.6, pp.1589-1596, 2007.
- Accelerated MU
- N. Gillis and F. Glineur, "Accelerated multiplicative updates and hierarchical ALS algorithms for nonnegative matrix factorization," Neural Computation, vol.24, no.4, pp.1085-1105, 2012.
- MU
-
PGD (projected gradient descent)
- PGD
- Direct PGD
- C.-J. Lin, "Projected gradient methods for nonnegative matrix factorization," Neural Computation, vol.19, no.10, pp.2756-2779, 2007.
-
ALS (alternative least squares)
- ALS
- Hierarchical ALS (HALS)
- A. Cichocki and P. Anh-Huy, "Fast local algorithms for large scale nonnegative matrix and tensor factorizations," IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol.92, no.3, pp.708-721, 2009.
- Accelerated Hierarchical ALS
- N. Gillis and F. Glineur, "Accelerated multiplicative updates and hierarchical ALS algorithms for nonnegative matrix factorization," Neural Computation, vol.24, no.4, pp.1085-1105, 2012.
-
ANLS (alternative non-negative least squares)
- ASGROUP (ANLS with Active Set Method and Column Grouping)
- ASGIVENS (ANLS with Active Set Method and Givens Updating)
- BPP (ANLS with Block Principal Pivoting Method)
- J. Kim, Y. He, and H. Park, "Algorithms for nonnegative matrix and tensor factorizations: A unified view based on block coordinate descent framework," Journal of Global Optimization, vol.58, no.2, pp.285-319, 2014.
- J. Kim and H. Park, "Fast nonnegative matrix factorization: An active-set-like method and comparisons," SIAM Journal on Scientific Computing (SISC), vol.33, no.6, pp.3261-3281, 2011.
-
-
Divergence-based
-
Div-MU
- MU
- D.D. Lee and H. S. Seung, "Algorithms for non-negative matrix factorization," NIPS 2000. (for Euclidean distance and Kullback-Leibler divergence (KL))
- A.Cichocki, S.Amari, R.Zdunek, R.Kompass, G.Hori, and Z.He, "Extended SMART algorithms for non-negative matrix factorization," Artificial Intelligence and Soft Computing, 2006. (for alpha divergence and beta divergence)
- MU
-
Div-ADMM
- D.L. Sun and C. Fvotte, "Alternating direction method of multipliers for non-negative matrix factorization with the beta divergence," IEEE ICASSP, 2014.
-
KL-FPA (First-order primal-dual algorithm)
- F. Yanez, and F. Bach, "Primal-dual algorithms for non-negative matrix factorization with the Kullback-Leibler divergence," IEEE ICASSP, 2017.
-
KL-BMD
- Block mirror descent method for KL-based non-negative matrix factorization
-
-
Semi
-
Semi-MU
- C.H.Q. Ding, T. Li, M. I. Jordan, "Convex and Semi-Nonnegative Matrix Factorizations," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.32, no.1, 2010.
-
Semi-BCD
- N. Gillis and A. Kumar, "Exact and Heuristic Algorithms for Semi-Nonnegative Matrix Factorization," SIAM Journal on Matrix Analysis and Applications 36 (4), pp. 1404-1424, 2015.
-
-
Variant
-
GNMF (Graph Regularized NMF)
- D. Cai, X. He, X. Wu, and J. Han, "Non-negative Matrix Factorization on Manifold," ICDM, 2008.
- D. Cai, X. He, J. Han and T. Huang, "Graph Regularized Non-negative Matrix Factorization for Data Representation," IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol.33, No.8, pp.1548-1560, 2011.
-
NeNMF (NMF with Nesterov's gradient acceleration)
- N. Guan, D. Tao, Z. Luo, and B. Yuan, "NeNMF: An Optimal Gradient Method for Non-negative Matrix Factorization," IEEE Transactions on Signal Processing, Vol.60, No.6, pp. 2882-2898, 2012.
-
SDNMF (NMF with Sinkhorn Distance)
- W. Qian, B. Hong, D. Cai, X. He, and X. Li, "Non-negative matrix factorization with sinkhorn distance," IJCAI, pp.1960-1966, 2016.
-
-
Robust
-
Robust-MU
- N. Guan, D. Tao, Z. Luo, and B. Yuan, "Online nonnegative matrix factorization with robust stochastic approximation," IEEE Transactions on Neural Networks and Learning Systems, 2012.
-
-
Sparse
-
Sparse-MU (Sparse multiplicative upates (MU))
- J. Eggert and E. Korner, "Sparse coding and NMF," IEEE International Joint Conference on Neural Networks, 2004.
- M. Schmidt, J. Larsen, and F. Hsiao, "Wind noise reduction using non-negative sparse coding," IEEE MLSP, 2007.
-
Sparse-MU-V
- T. Virtanen, "Monaural sound source separation by non-negative factorization with temporal continuity and sparseness criteria," IEEE Transactions on Audio, Speech, and Language Processing, vol.15, no.3, 2007.
-
sparseNMF (Sparse NMF)
-
SC-NMF (NMF with sparseness constraints)
- Patrik O. Hoyer, "Non-negative matrix factorization with sparseness constraints," Journal of Machine Learning Research (JMLR), vol.5, pp.1457-1469, 2004.
-
Nonsmooth-NMF
- A. Pascual-Montano, J. M. Carazo, K. Kochi, D. Lehmann, and R. D. Pascual-Marqui, "Nonsmooth Nonnegative Matrix Factorization (nsNMF)," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.28, no.3, pp.403-415, 2006.
-
NS-NMF (Fast nonsmooth NMF)
- Z. Yang, Y. Zhang, W. Yan, Y. Xiang, and S. Xie, "A fast non-smooth nonnegative matrix factorization for learning sparse representation," IEEE Access, vol.4, pp.5161-5168, 2016.
-
Proj-Sparse
- P. O. Hoyer, "Non-negative matrix factorization with sparseness constraints," Journal of Machine Learning Research (JMLR), vol.5, pp.1457-1469, 2004.
- R. Ohib, N. Gillis, Niccolò Dalmasso, S. Shah, V. K. Potluru, S. Plis, "Explicit Group Sparse Projection with Applications to Deep Learning and NMF," arXiv preprint:1912.03896, 2019.
-
PALM-Sparse-Smooth-NMF
- PALM framework with smoothness and sparsity constraints for non-negative matrix factorization.
-
-
Orthogonal
-
DTPP (Orthogonal multiplicative upates (MU))
- C. Ding, T. Li, W. Peng, and H. Park, "Orthogonal nonnegative matrix t-factorizations for clustering," ACM KDD, 2006.
-
Orth-MU (Orthogonal multiplicative upates (MU))
- S. Choi, "Algorithms for orthogonal nonnegative matrix factorization." IEEE IJCNN, 2008.
-
ALT-ONMF
- F. Pompilia, N. Gillis, P.-A. Absil, and F. Glineur, "Two algorithms for orthogonal nonnegative matrix factorization with application to clustering," Neurocomputing, vol.141, no.2, pp.15-25, 2014.
-
HALS-SO (Hierarchical ALS with soft orthogonal constraint)
- M. Shiga, K. Tatsumi, S. Muto, K. Tsuda, Y. Yamamoto, T. Mori, and T. Tanji, "Sparse modeling of EELS and EDX spectral imaging data by nonnegative matrix factorization," Ultramicroscopy, Vol.170, p.43-59, 2016.
-
-
Symmetric
-
SymmANLS (Symmetric ANLS)
-
D. Kuang, C. Ding, H. Park, "Symmetric Nonnegative Matrix Factorization for Graph Clustering," SIAM SDM'12, 2012.
-
D. Kuang, S. Yun, H. Park, "SymNMF Nonnegative low-rank approximation of a similarity matrix for graph clustering," Journal of Global Optimization, vol.62, no.3, pp.545-574, 2015.
-
Z. Zhu, X. Li, K. Liu, Q. Li, "Dropping Symmetry for Fast Symmetric Nonnegative Matrix Factorization," NIPS, 2018.
-
-
SymmHALS (Symmetric HALS)
- Z. Zhu, X. Li, K. Liu, Q. Li, "Dropping Symmetry for Fast Symmetric Nonnegative Matrix Factorization," NIPS, 2018.
-
SymmNewton (Symmetric Newton)
-
-
Online/stochastic
-
Incremental-MU and Online-MU
- S. S. Bucak and B. Gunsel, "Incremental Subspace Learning via Non-negative Matrix Factorization," Pattern Recognition, 2009.
-
SPG (Stochastic projected gradient descent)
-
Robust-Online-MU (Robust online NMF)
- R. Zhao and Y. F. Tan, "Online nonnegative matrix factorization with outliers," IEEE ICASSP2016, 2016.
- N. Guan, D. Tao, Z. Luo, and B. Yuan, "Online nonnegative matrix factorization with robust stochastic approximation," IEEE Transactions on Newral Network Learninig Systems, 2012.
-
ASAG-MU-NMF (Asymmetric stochastic averaging gradient multiplicative updates)
- R. Serizel, S. Essid and G.Richard, "Mini-batch stochastic approaches for accelerated multiplicative updates in nonnegative matrix factorisation with beta-divergence," IEEE MLSP, 2016.
-
SVRMU-NMF (Stochastic multiplicative updates) and SVRMU (Stochastic variance reduced multiplicative updates)
- H. Kasai, "Stochastic variance reduced multiplicative update for nonnegative matrix factorization," IEEE ICASSP, 2018.
-
SAGMU-NMF (Stochastic averaging gradient multiplicative multiplicative updates)
- H. Kasai, "Accelerated stochastic multiplicative update with gradient averaging for nonnegative matrix factorizations," EUSIPCO, 2018.
-
-
Probabilistic
-
PNMF-GIBBS (Gibbs sampler for non-negative matrix factorisation, with ARD.) (not included)
-
M. N. Schmidt, O. Winther, L.K. Hansen, "Bayesian non-negative matrix factorization," International Conference on Independent Component Analysis and Signal Separation, Springer Lecture Notes in Computer Science, Vol. 5441, 2009.
-
T. Brouwer, P. Lio, "Bayesian Hybrid Matrix Factorisation for Data Integration," AISTATS, 2017.
-
-
PNMF-VB (Variational Bayesian inference for non-negative matrix factorisation, with ARD)
- T. Brouwer, J. Frellsen. P. Lio, "Comparative Study of Inference Methods for Bayesian Nonnegative Matrix Factorisation," ECML PKDD, 2017.
-
Prob-NMF
-
-
Deep
-
Deep-Semi and Deep-Bidir-Semi
-
G. Trigeorgis, K. Bousmalis, S. Zafeiriou and B. Schuller, "A deep semi-NMF model for learning hidden representations," ICML, 2014.
-
G. Trigeorgis, K. Bousmalis, S. Zafeiriou and B. Schuller, "A deep matrix factorization method for learning attribute representations," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.39, no.3, pp.417-429, 2017.
-
-
Deep-nsNMF
-
Deep-Multiview-Semi
- H. Zhao, Z. Ding, and Y. Fu, "Multi-view clustering via deep matrix factorization," AAAI, 2017.
-
-
Convex
-
Convex-MU and Kernel-Convex-MU
-
C. Ding, T. Li, and M.I. Jordan, "Convex and semi-nonnegative matrix factorizations," IEEE Transations on Pattern Analysis and Machine Intelligence, vol. 32, no. 1, pp. 45-55, 2010.
-
T. Li and C. Ding, "The relationships among various nonnegative matrix factorization methods for clustering," ICDM, 2006.
-
Y. Li and A. Ngom, "A new kernel non-Negative matrix factorization and its application in microarray data analysis," CIBCB, 2012.
-
-
-
Separable
-
SPA
- N. Gillis and S.A. Vavasis, "Fast and robust recursive algorithms for separable nonnegative matrix factorization," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.36, no.4, pp.698-714, 2014.
-
SNPA
- N. Gillis, "Successive nonnegative projection algorithm for robust nonnegative blind source separation," SIAM Journal on Imaging Sciences, vol.7, no.2, pp.1420-1450, 2014.
-
-
Convolutive
-
MU-Conv
- Multiplicative update (MU) based convolutive non-negative matrix factorization
-
Heur-MU-Conv
- Heuristic multiplicative update (MU) based convolutive non-negative matrix factorization
-
ADMM-Y-Conv
- ADMM based convolutive non-negative matrix factorization
-
ADMM-Seq-Conv
- ADMM based convolutive non-negative matrix factorization
-
-
Projective
- projectiveNMF
- Z. Yang, and E. Oja, "Linear and nonlinear projective nonnegative matrix factorization," IEEE Transactions on Neural Networks, 21(5), pp.734-749, 2010.
- projectiveNMF
-
Rank2
- Rank2-NMF
- N, Gillis, "Nonnegative Matrix Factorization," SIAM, 2020.
- Rank2-NMF
-
Nonnegative matrix tri-factorization
- Sep-Symm-NMTF
- S. Arora, R. Ge, Y. Halpern, D. Mimno, A. Moitra, D. Sontag, Y. Wu, M. Zhu, "A practical algorithm for topic modeling with provable guarantees," ICML, 2013.
- Sep-Symm-NMTF
-
Nonnegative under-approximation
- Recursive-NMU (Recursive non-negative matrix underapproximation)
-
N. Gillis and F. Glineur, "Using underapproximations for sparse nonnegative matrix factorization," Pattern Recognition, vol.43, no.4, pp.1676-1687, 2010.
-
N. Gillis and R.J. Plemmons, "Dimensionality reduction, classification, and spectral mixture analysis using nonnegative underapproximationm," Optical Engineering 50, 027001, 2011.
-
- Recursive-NMU (Recursive non-negative matrix underapproximation)
-
Minimum-volume
- minvol-NMF
- V. Leplat, A.M.S. Ang, N. Gillis, "Minimum-volume rank-deficient nonnegative matrix factorizations," IEEE ICASSP, 2019.
- minvol-NMF
-
Weighted Low-Rank matrix approximation
- WLRA
| Category | Name in example codes | function | options.alg |
other options |
|---|---|---|---|---|
| Frobenius-norm | Fro-MU | fro_mu_nmf |
mu |
metric='euc' |
| Modified Fro-MU | fro_mu_nmf |
mod_mu |
||
| Accelerated Fro-MU | fro_mu_nmf |
acc_mu |
||
| PGD | pgd_nmf |
pgd |
||
| Direct PGD | pgd_nmf |
direct_pgd |
||
| Adaptive-step PGD | pgd_nmf |
adp_step_pgd |
||
| ALS | als_nmf |
als |
||
| Hierarchical ALS | als_nmf |
hals_mu |
||
| Accelerated Hierarchical ALS | als_nmf |
acc_hals_mu |
||
| ASGROUP | anls_nmf |
anls_asgroup |
||
| ASGIVENS | anls_nmf |
anls_asgivens |
||
| BPP | anls_nmf |
anls_bpp |
||
| Divergence | Div-MU-KL | div_mu_nmf |
metric='kl-div' |
|
| Div-MU-ALPHA | div_mu_nmf |
metric='alpha-div' |
||
| Div-MU-BETA | div_mu_nmf |
metric='beta-div' |
||
| Div-MU-IS | div_mu_nmf |
metric='beta-div' d_beta=0 |
||
| Div-MU-KL | div_mu_nmf |
metric='beta-div' d_beta=1 |
||
| Div-ADMM-IS | div_admm_nmf |
metric='beta-div' d_beta=0 |
||
| Div-ADMM-KL | div_admm_nmf |
metric='beta-div' d_beta=1 |
||
| KL-FPA | kl_fpa_nmf |
|||
| KL-BMD | kl_bmd_nmf |
|||
| Semi | Semi-MU | semi_mu_nmf |
||
| Semi-BCD | semi_bcd_nmf |
|||
| Variant | NeNMF | nenmf |
||
| GNMF | GNMF |
|||
| SDNMF | SDNMF |
|||
| Robust | Robust-MU | robust_mu_nmf |
||
| Sparse | Sparse-MU-EUC | sparse_mu_nmf |
metric='euc' |
|
| Sparse-MU-KL | sparse_mu_nmf |
metric='kl-div' |
||
| sparseNMF | sparse_nmf |
|||
| SC-NMF | sc_nmf |
|||
| Nonsmooth-NMF | ns_nmf |
metric='euc', update_alg='apg' |
||
| Proj-Sparse | proj_sparse_nmf |
|||
| PALM-Sparse-Smooth | palm_sparse_smooth_nmf |
|||
| Orthogonal | DTPP | dtpp_nmf |
||
| Orth-MU | orth_mu_nmf |
|||
| NMF-HALS-SO | hals_so_nmf |
|||
| ALT-ONMF | alternating_onmf |
|||
| Symmetric | SymmANLS | symm_anls |
||
| SymmHALS | symm_halsacc |
|||
| SymmNewton | symm_newton |
|||
| Online | Incremental-NMF | incremental_mu_nmf |
||
| Online-MU | online_mu_nmf |
|||
| Accelerated Online-MU | acc_online_mu_nmf |
|||
| SPG | spg_nmf |
|||
| Robust-Online-MU | robust_online_mu_nmf |
|||
| ASAG-MU-NMF | asag_mu_nmf |
|||
| Stochastic-MU | smu_nmf |
|||
| SVRMU | svrmu_nmf |
|||
| R-SVRMU | svrmu_nmf |
robust=true |
||
| SAGMU | sagmu_nmf |
|||
| Probabilistic | PNMF-VB | vb_pro_nmf |
||
| PNMF-VB-ARD | vb_pro_nmf |
ard=true |
||
| Prob-NM | prob_nmf |
|||
| Deep | Deep-Semi | deep_semi_nmf |
||
| Deep-Bidir-Semi | deep_bidirectional_nmf |
|||
| Deep-nsNMF | deep_ns_nmf |
|||
| Deep-Multiview-Semi | deep_multiview_semi_nmf |
|||
| Convex | Convex-MU | convex_mu_nmf |
sub_mode='std' |
|
| Kernel-Convex-MU | convex_mu_nmf |
sub_mode='kernel' |
||
| Separable | SPA | spa |
||
| SNPA | snpa |
|||
| Convolutive | MU-Conv | mu_conv_nmf |
||
| Heur-MU-Conv | heuristic_mu_conv_nmf |
|||
| ADMM-Y-Conv | admm_y_conv_nmf |
|||
| ADMM-Seq-Conv | admm_seq_conv_nmf |
|||
| Rank2 | Rank2-NMF | rank2nmf |
||
| Nonnegative matrix tri-factorization | Sep-Symm-NMTF | sep_symm_nmtf |
||
| Nonnegative under-approximation | recursive_nmu | recursive_nmu |
||
| Minimum-volume | minvol-NMF | minvol_nmf |
||
| Weighted Low-Rank matrix approximation | WLRA | wlra |
./ - Top directory.
./README.md - This readme file.
./run_me_first.m - The scipt that you need to run first.
./demo.m - Demonstration script to check and understand this package easily.
./demo_face.m - Demonstration script to check and understand this package easily.
./demo.py - Demonstration script to use this package easily from python.
|plotter/ - Contains plotting tools to show convergence results and various plots.
|auxiliary/ - Some auxiliary tools for this project.
|solver/ - Contains various optimization algorithms.
|--- frobenius_norm/ - NMF solvers with Frobenius norm metric.
|--- divergence/ - NMF solvers with various divertence metrics (KL, beta, alpha, IS).
|--- online/ - Online/stochstic NMF solvers.
|--- sparse/ - Sparse NMF solvers.
|--- robust/ - Robust NMF solvers.
|--- orthogonal/ - Orthogonal NMF solvers.
|--- symmetric/ - Symmetric NMF solvers.
|--- semi/ - Semi NMF solvers.
|--- deep/ - Deep NMF solvers.
|--- probabilistic/ - Probabilistic NMF solvers.
|--- convex/ - Convex NMF solver.
|--- convolutive/ - Convolutive NMF solvers.
|--- minvol/ - Minimum-volume rank-deficient NMF.
|--- nm_under_approx/ - Recursive non-negative matrix underapproximation.
|--- nmtf/ - Separable symmetric nonnegative matrix tri-factorization.
|--- projective_nmf/ - Projective NMF solver.
|--- rank2/ - rank-two NMF solver.
|--- weight_lowrank_aprox/ - Weighted Low-Rank matrix Approximation algorithm.
|--- nenmf/ - Nesterov's accelerated NMF solver.
|--- nnls/ - Solvers for nonnegativity-constrained least squares.
|--- 3rd_party/ - Solvers provided by 3rd_party.
|--- solver_health_check.m - Health check scripts for solvers.
|applications/ - Some appplications using NMF.
Run run_me_first for path configurations.
%% First run the setup script
run_me_first; Just execute demo for the simplest demonstration of this package. .
%% Execute the demonstration script
demo; The "demo.m" file contains below.
%% generate synthetic data non-negative matrix V size of (mxn)
m = 500;
n = 100;
V = rand(m,n);
%% Initialize rank to be factorized
rank = 5;
%% perform factroization
% Fro-MU
options.alg = 'mu';
[w_mu, infos_mu] = fro_mu_nmf(V, rank, options);
% Hierarchical ALS
options.alg = 'hals';
[w_hals, infos_hals] = als_nmf(V, rank, options);
%% plot
display_graph('epoch','cost', {'MU', 'HALS'}, {w_mu, w_hals}, {infos_mu, infos_hals});
Let's take a closer look at the code above bit by bit. The procedure has only 4 steps!
Step 1: Generate data
First, we generate synthetic data of V of size (mxn).
m = 500;
n = 100;
V = rand(m,n);Step 2: Define rank
We set the rank value.
rank = 5;Step 3: Perform solver
Now, you can perform nmf solvers, e.g., Frobenius-norm MU and Hierarchical ALS (HALS), calling solver functions, i.e., fro_mu_nmf() function and als_nmf() function after setting some optimization options.
% Fro-MU
options.alg = 'mu';
[w_mu, infos_mu] = fro_mu_nmf(V, rank, options);
% Hierarchical ALS
options.alg = 'hals';
[w_hals, infos_hals] = als_nmf(V, rank, options); They return the final solutions of w and the statistics information that include the histories of epoch numbers, cost values, norms of gradient, the number of gradient evaluations and so on.
Step 4: Show result
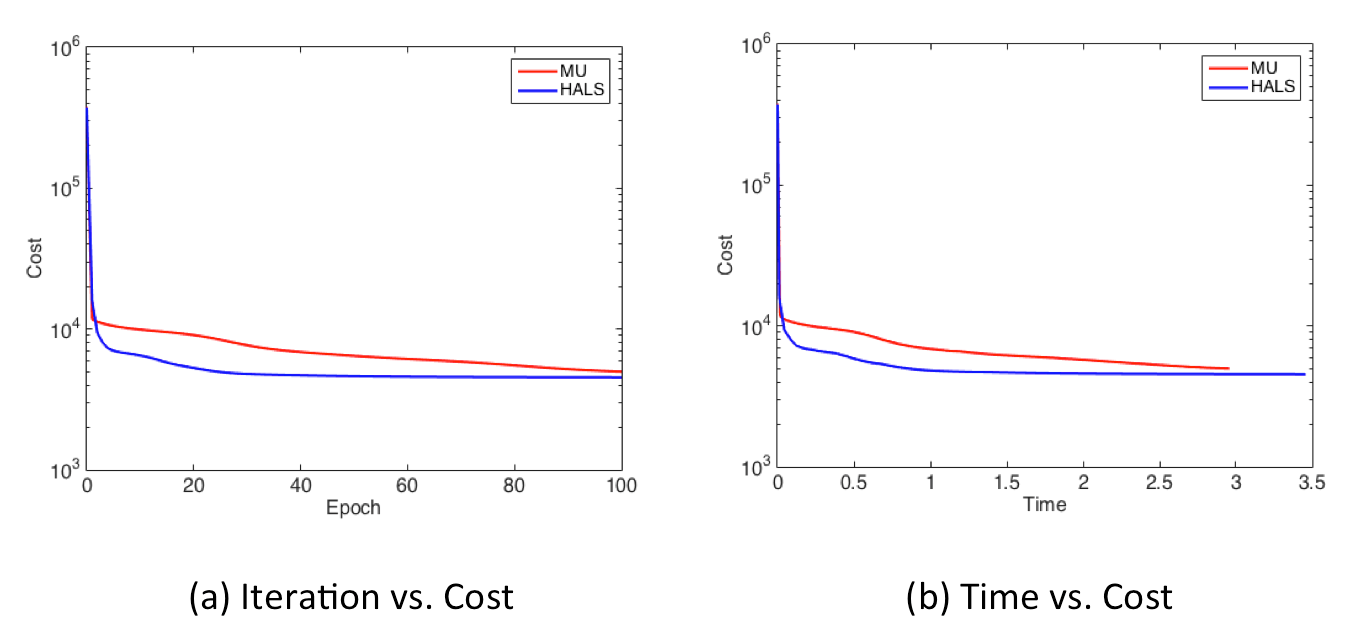
Finally, display_graph() provides output results of decreasing behavior of the cost values in terms of the number of iterrations (epochs) and time [sec].
display_graph('epoch','cost', {'Fro-MU', 'HALS'}, {w_mu, w_hals}, {infos_mu, infos_hals});
display_graph('time','cost', {'Fro-MU', 'HALS'}, {w_mu, w_hals}, {infos_mu, infos_hals});That's it!
"demo_face.m" illustrates the learned basis (dictrionary) in case of CBCL face datasets.
The dataset is first loaded into V instead of generating synthetic data in Step 1.
V = importdata('./data/CBCL_face.mat');Then, we can display basis elements (W: dictionary) obtained with different algorithms additionally in Step 4.
plot_dictionnary(w_mu.W, [], [7 7]);
plot_dictionnary(w_hals.W, [], [7 7]); Step 1: Find the path to the MATLAB folder
Run matlabroot in the MATLAB command window.
matlabroot; Step 2: Install the Engine API
To install the engine API, choose one of the following. You must call this python install command in the specified folder. The followings are examples in case of R2022a.
- Windows
cd "c:\Program Files\MATLAB\R2022a\extern\engines\python"
python setup.py install
- Linux
cd "/usr/local/MATLAB/R2022a/bin/matlab/extern/engines/python"
python setup.py install
- macOS
cd "/Applications/MATLAB_R2022a.app/extern/engines/python"
python setup.py install
Step 3: Run demonstration code
python demo.py
As for Steps 1 and 2, see more details here.
- The NMFLibrary is free, non-commercial and open source.
- The code provided iin NMFLibrary should only be used for academic/research purposes.
- Third party files are ported and included as is.
- Many solvers (
fro_mu_nmf.m,als_nmf.m,wlra.m,spa.m,snpa.m,proj_sparse_nmf.m,rank2nmf.m,projective_nmf.m,alternating_onmf.m,recursive_nmu.m,sep_symm_nmtf.m,minvol_nmf.m,nnls_*.m,semi_bcd_nmf.mand others) are ported from the codes of NMF book written by Nicolas Gillis. - For ANLS algorithms:
nnlsm_activeset.m,nnls1_asgivens.m,nnlsm_blockpivot.m, andnormalEqComb.mwritten by Jingu Kim. - For PGD algorithm:
nlssubprob.m. - For GNMF algorithm:
GNMF.m,GNMF_Multi.m,constructW.mandlitekmeans.mwrittnen by Deng Cai. - For SDNMF algorithm:
SDNMF.mandSDNMF_Multi.mwrittnen by Wei Qian. - For Symmetric algorithms writtnen by D.Kang et al. and Z. Zhu et al.
- For KL-FPA algorithm:
kl_fpa_nmf.mwrittnen by Felipe Yanez. - For KL-BMD algorithm:
BMD.mwrittnen by by LTK Hien. - For Deep algorithm:
deep_semi_nmf.m, deep_bidirectional_nmf.m` writtnen by G.Trigeorgis, and 'deep_multiview_semi_nmf.m' writtnen by H.Zhao. - For PALM-Sparse-Smooth algorithm:
palm_sparse_smooth_nmf.mwrittnen by Raimon Fabregat. - For Convex-MU algorithm:
convex_mu_nmf.mwrittnen by Yifeng Li. - For Convolutive algorithm:
mu_conv_nmf.m,heuristic_mu_conv_nmf.m,admm_y_conv_nmf.m, andadmm_seq_conv_nmf.mwrittnen by lyn202206. - For Probabilistic algorithm:
prob_nmf.mby NMF DTU Toolbox, Lars Kai Hansen. - For Probabilistic algorithm: vb_pro_nmf.m` is ported from the Python code originally written by T. Brouwer et. al..
- For dictionaly visualization:
plot_dictionnary.m,rescale.m, andgetoptions.m.
- Many solvers (
- Thank you for big contributions to this library to
- Haonan Huang
- Mitsuhiko Horie
- Takumi Fukunaga
If you have any problems or questions, please contact the author: Hiroyuki Kasai (email: hiroyuki dot kasai at waseda dot jp)
- Version 2.1 (July 22, 2022)
- No-option is allowed in all solvers.
- A python demonstration script is added.
- Application scripts are added.
- Version 2.0 (July 18, 2022)
- Major update.
- New NMF models are added.
- New NMF solvers are added.
- Code structure of solvers is refactored.
- Else
- Solver/user-defined stopping function is supported.
- Statistics display module is refactored.
- Acceleration algorithms on frobenius-norm based methods are added.
- Divergence-based methods are separated from frobenius-norm based methods.
- Version update checking mechanism is supported.
- Demonstration script to use this package from python is included.
- Version 1.8.1 (Oct. 14, 2020)
- Bug fixed in sc_nmf.m and semi_mu_nmf, and added the LPinitSemiNMF algorithm into generate_init_factors.m (Thanks to Haonan Huang).
- Version 1.7.0 (June 27, 2019)
- Symmetic solvers are added.
- Clustering quality measurements are integrated into store_nmf_info.m.
- Version 1.7.0 (May 21, 2019)
- PNMF-VB and NeNMF are added.
- Fixed some bugs.
- Version 1.6.0 (May 16, 2019)
- DTPP is added.
- Version 1.5.1 (Apr. 22, 2019)
- Some solvers are modified to fix bugs.
- Version 1.5.0 (July 30, 2018)
- fnsNMF and NMF-HALS-SO are added.
- Version 1.4.0 (July 24, 2018)
- sparseMU and orthMU are added.
- MU with Kullback-Leibler divergence (KL), Amari alpha divergence, and beta divergenceare added.
- Version 1.3.0 (July 23, 2018)
- SC-NMF, scNMF and csNMF are added.
- Version 1.2.0 (July 21, 2018)
- GNMF, Semi-NMF and SDNMF are added.
- Version 1.1.0 (Apr. 17, 2018)
- Online/stochastic solvers are added.
- Version 1.0.0 (Apr. 04, 2017)
- Initial version.