Check out the new online solver! Let me know what you think. I will be continuing to make minor improvements in the coming weeks.
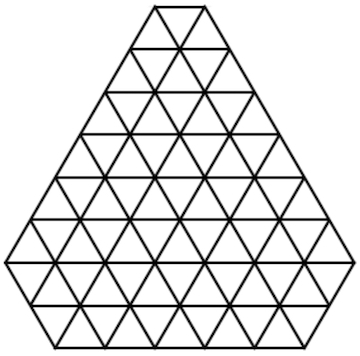
This repository documents manually discovered solutions to my triangle puzzle. The goal is to fit the 12 pieces into the given frame, as shown below. I've called it the triangle puzzle because each piece can be constructed out of 6 equilateral triangles. Notably, the 12 pieces represent ALL possible arrangements of 6 equilateral triangles joined edge-to-edge on a triangular grid, a.k.a. "hexiamonds".
I've had this puzzle for most of my life, and started documenting solutions around 2002. Thanks to David Goodger's Polyform Puzzler site, we know the total number of solutions is 5885. This was recently reconfirmed by user kqyrt's comprehensive solution list, which contains 11770 solutions including mirror images.
I created this repo in 2018 to more efficiently document new solutions and programmatically check if they had already been discovered. At that time, I had discovered about 400 unique solutions and never found a repeat. The first repeat was found in September 2018.
Many solutions have sister solutions reachable by flipping or rotating a group of pieces that forms a symmetric shape, swapping two groups of pieces that form the same shape, or otherwise adjusting the original. I've identified sisters by providing both an ID and a sub-ID for each solution; sister solutions share the same ID. There is no formal definition of how major a transformation has to be to qualify as a new solution instead of a sister solution: but ultimately it doesn't really matter if you just want to know how many unique solutions there are. I've generally considered any solution found by looking at an existing solution as a sister solution to that one.
If you find a new solution with the online solver, a message will pop up showing an encoded version of your solution. The key to the encoding of this puzzle is that the frame can be broken down into 72 triangles:
Solutions are recorded as 72-character strings. Each character corresponds to 1 triangle in the frame, and indicates which piece covers that triangle based on the piece IDs shown below. The solution describes the triangles in each row from left to right, top to bottom: the first three characters correspond to the three triangles in the first row, etc.
Example solution and corresponding encoding:
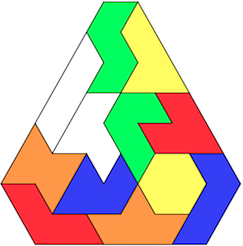
|
77b
977bb
9977bbb
993311100
49333110000
4444232155588
6642222a55588
6666aaaaa88
|
You're welcome to file an issue reporting a new solution and I will take care of entering it in the system. However, if you want to do it yourself, you can clone the repo and add your solution using puzzle.ipynb. While it is technically possible to enter a solution directly into solutions.csv, it's critical that solutions be entered with Python to ascertain that the solution has not already been discovered.
You will need a Python 3 environment with matplotlib and jupyter:
pip install matplotlib
pip install jupyter
Open the Jupyter notebook (run jupyter notebook in the repo's root). Run the first cell, then fill in author name, date, and solution in the second cell and run it. There are a few options for what the output looks like:
-
An illustration of the solution you've entered, along with a summary of the other parameters you've entered and an input field with the text "Press enter if good". Success! Please review the illustration and parameters. If you need to change something, type anything in the input field (I like "no" or "asdf") and the solution won't be recorded yet. Otherwise, just hit enter and your solution will be added to
solutions.csv. -
Same as above, except with text "WARNING: Did not pass basic check" and no input field. This means your solution is invalid. Please check your solution input and the illustration and try again.
-
An empty frame and an error message resulting from an invalid parameter. Hopefully those messages should be pretty clear, but if not, let me know by filing an issue - it's possible the parameter verification code has a bug.
-
(And I can't fully rule out) a stack trace. If this happens, please file an issue with your stack trace and parameters so I can fix it. If you want to debug it yourself, great, but please notify me of the bug. Feel free to do so by opening a pull request with your fix! ;)
As mentioned above, two people have independently found the total number of solutions to be 5885. David Goodger's code is available here. (He also has ideas about expanding his project here if you're interested in getting involved, although that page was last updated in 2015.)
If you feel like writing code to recompute the solution set, I'm happy to hear about a third confirmation of the solution count. I will mention you and your code (if published) in the readme. However, please do not use this repo as your workspace or add computer-generated solutions to solutions.csv.