-
Notifications
You must be signed in to change notification settings - Fork 129
Covariant Expressions for Vector and Tensor Operators
This page summarizes the covariant expressions for vector and tensor operators used in Athena++. These operators are mostly used for computing viscosity and thermal conduction terms in Diffusion Processes. Please see Appendix A of Stone & Norman (1992) for details.
The metric tensor for orthogonal coordinate systems reads
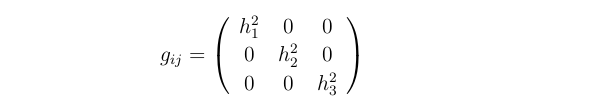
where h1, h2, and h3 are scale factors or Lamé coefficients. They take different forms depending on the specific coordinate system (see Table 1 below).
Table 1: Scale factors and their derivatives in various coordinate systems.
| scale factors | Cartesian | Cylindrical | Spherical |
|---|---|---|---|
| h1 | 1 | 1 | 1 |
| h2 | 1 | r | r |
| h3 = h31 · h32 | 1 | 1 | r · sinθ |
| h31 | 1 | 1 | r |
| h32 | 1 | 1 | sinθ |
| ∂h2 / ∂x1 | 0 | 1 | 1 |
| ∂h31 / ∂x1 | 0 | 0 | 1 |
| ∂h32 / ∂x2 | 0 | 0 | cosθ |
∇ Φ = ∂Φ / (hi ∂xi) êi ,
with i ∈ [x1,x2,x3] and assuming Einstein summation (the repeated indices are implicitly summed over).
∇ · F = g-½ ∂(g½ Fi / hi) / ∂xi,
where F = Fi êi , and g½ = h1h2h3.
∇ × F = hk g-½; ϵkji ∂(hi Fi) / ∂xj êi.
∇ F = [∂(hiFi) / ∂xj - Γki j hk Fk] (hi hj)-1 êi êj ,
where Γki j is the Christoffel symbol:
Γii i = (2hi2)-1 ∂ hi2 / ∂ xi
Γii j = Γij i = (2hi2)-1 ∂ hi2 / ∂ xj
Γij j = -(2hi2)-1 ∂ hj2 / ∂ xi
Γij k = 0
For instance, the viscous stress tensor (neglecting the bulk viscosity) can be written as
σi j = -μ( vi; j + vj; i -⅔ vk;k gi j ),
where μ = ρ ν is the dynamic viscosity. The expression consists of two gradient terms and one term containing the divergence of the velocity. All of these terms can be calculated in any of the supported Coordinate Systems and Meshes using the above formulae.
Getting Started
User Guide
- Configuring
- Compiling
- The Input File
- Problem Generators
- Boundary Conditions
- Coordinate Systems and Meshes
- Running the Code
- Outputs
- Using MPI and OpenMP
- Static Mesh Refinement
- Adaptive Mesh Refinement
- Load Balancing
- Special Relativity
- General Relativity
- Passive Scalars
- Shearing Box
- Diffusion Processes
- General Equation of State
- FFT
- Multigrid
- High-Order Methods
- Super-Time-Stepping
- Orbital Advection
- Rotating System
- Reading Data from External Files
- Non-relativistic Radiation Transport
- Cosmic Ray Transport
- Units and Constants
Programmer Guide