Towards scalable solutions for boolean satisfiability
Solving boolean satisfiability in polynomial time proves P = NP. Yet, state-of-the-art neural SAT solvers have <1M parameters and the largest dataset has 120k examples. Indeed, neural approaches to SAT remain far behind their classical/heuristic counterparts.
Maybe we haven't thrown enough GPUs at SAT? And maybe post hoc interpretability work can extract novel discrete algorithms for SAT?
I wonder whether the dominance of tough-to-scale (but mathematically intuitive) GNN approaches to neural SAT is akin to syntax-based (but linguistically intuitive) approaches to language modeling prior to the transformer.
I also notice this correspondence between SAT <-> transformer:
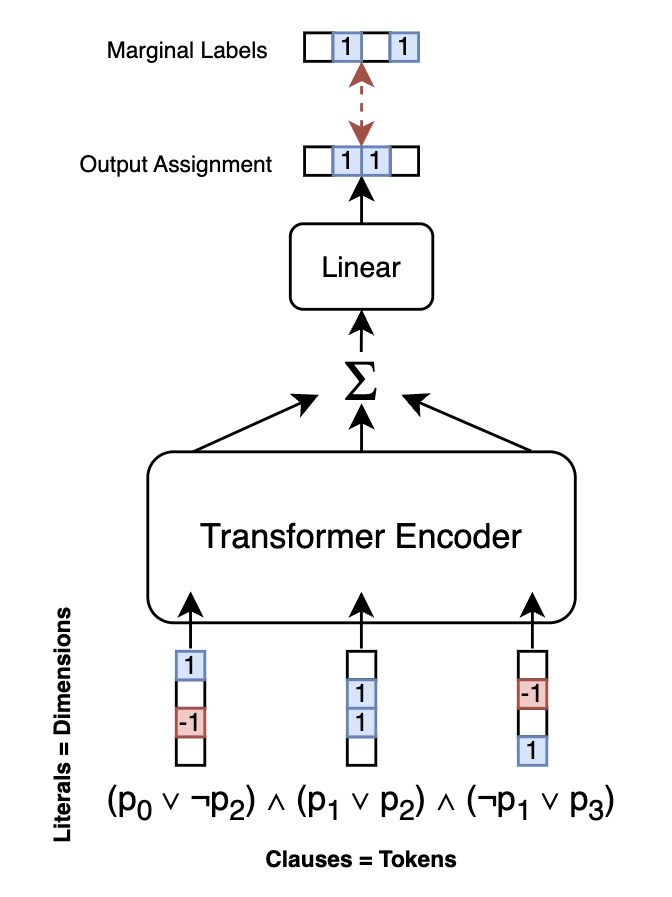
- variable count <-> embedding dimensionality
- clause <-> token
- clause count <-> sequence length
- satisfiability <-> classification
In this setting, we don't need position embeddings since clause conjunction is order-invariant. Each clause embedding is a variable-count-dimensional sparse vector with (n-SAT) n elements either 1 or -1 (negated). Furthermore, we can train for either SAT solving by training output of the SumPool against marginal labels or for SAT/UNSAT classification by adding a binary classification head on top of the SumPool.
I use the 3 data generation algorithms implemented for NSNet (SR, 3-SAT, and CA) and simply scale up the amount of generated data and provide them on HuggingFace. I also leverage the negation approach in NeuroSAT to generate UNSAT counterparts for examples produced by SR. To generate the data:
git clone https://github.com/KhoomeiK/SATScale
cd SATScale/NSNet
poetry install
poetry run huggingface-cli login
poetry run sh scripts/sat_data.sh
Be sure to log in with your HuggingFace token if you want to upload the generated data to your dataset hub.