MortalityTables

A Julia package for working with MortalityTables. Has:

• Full set of SOA mort.soa.org tables included
• survival and decrement functions to calculate decrements over period of time
• Partial year mortality calculations (Uniform, Constant, Balducci)
• Friendly syntax and flexible usage
• Extensive set of parametric mortality models.

On this Page:

• Examples
  • Quickstart
  • Quickly access and compare tables
  • Scaling and capping rates
• Fractional Years
• Tables
  • mort.SOA.org Tables
  • From CSV
  • From XTbML
  • Custom Tables
• Parameterized Models

Examples

Quickstart

Load and see information about a particular table:

julia> vbt2001 = MortalityTables.table("2001 VBT Residual Standard Select and Ultimate - Male Nonsmoker, ANB")
MortalityTable (Insured Lives Mortality):
   Name:
       2001 VBT Residual Standard Select and Ultimate - Male Nonsmoker, ANB
   Fields:
       (:select, :ultimate, :metadata)
   Provider:
       Society of Actuaries
   mort.SOA.org ID:
       1118
   mort.SOA.org link:
       https://mort.soa.org/ViewTable.aspx?&TableIdentity=1118
   Description:
       2001 Valuation Basic Table (VBT) Residual Standard Select and Ultimate Table -  Male Nonsmoker.
       Basis: Age Nearest Birthday. 
       Minimum Select Age: 0. 
       Maximum Select Age: 99. 
       Minimum Ultimate Age: 25. 
       Maximum Ultimate Age: 120

The package revolves around easy-to-access vectors which are indexed by attained age:

julia> vbt2001.select[35]          # vector of rates for issue age 35
 0.00036
 0.00048
 ⋮
 0.94729
 1.0
 
julia> vbt2001.select[35][35]      # issue age 35, attained age 35
 0.00036
 
julia> vbt2001.select[35][50:end] # issue age 35, attained age 50 through end of table
0.00316
0.00345
 ⋮
0.94729
1.0

julia> vbt2001.ultimate[95]        # ultimate vectors only need to be called with the attained age
 0.24298

Calculate the force of mortality or survival over a range of time:

julia> survival(vbt2001.ultimate,30,40) # the survival between ages 30 and 40
0.9894404665434904

julia> decrement(vbt2001.ultimate,30,40) # the decrement between ages 30 and 40
0.010559533456509618

Non-whole periods of time are supported when you specify the assumption (Constant(), Uniform(), or Balducci()) for fractional periods:

julia> survival(vbt2001.ultimate,30,40.5,Uniform()) # the survival between ages 30 and 40.5
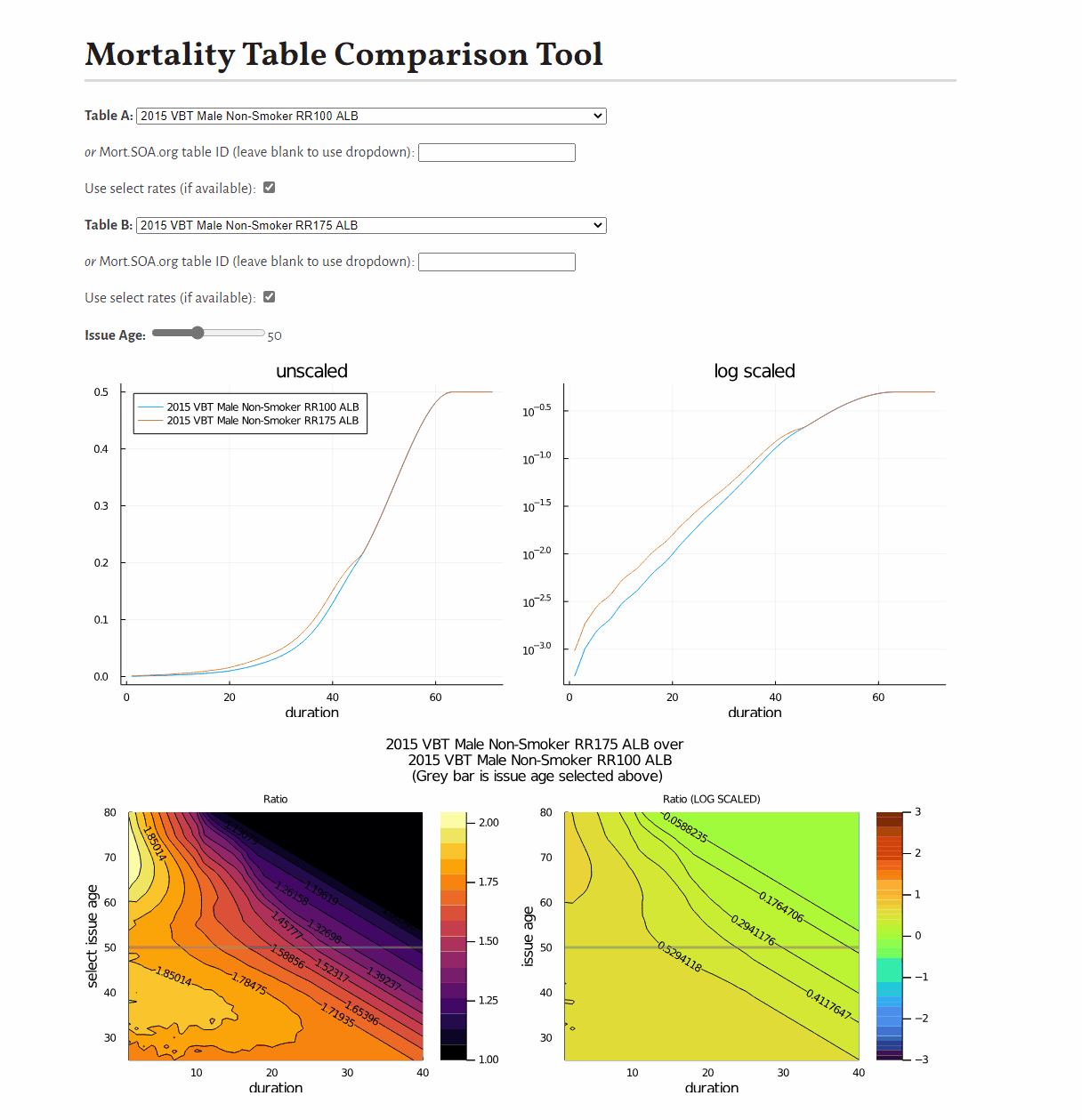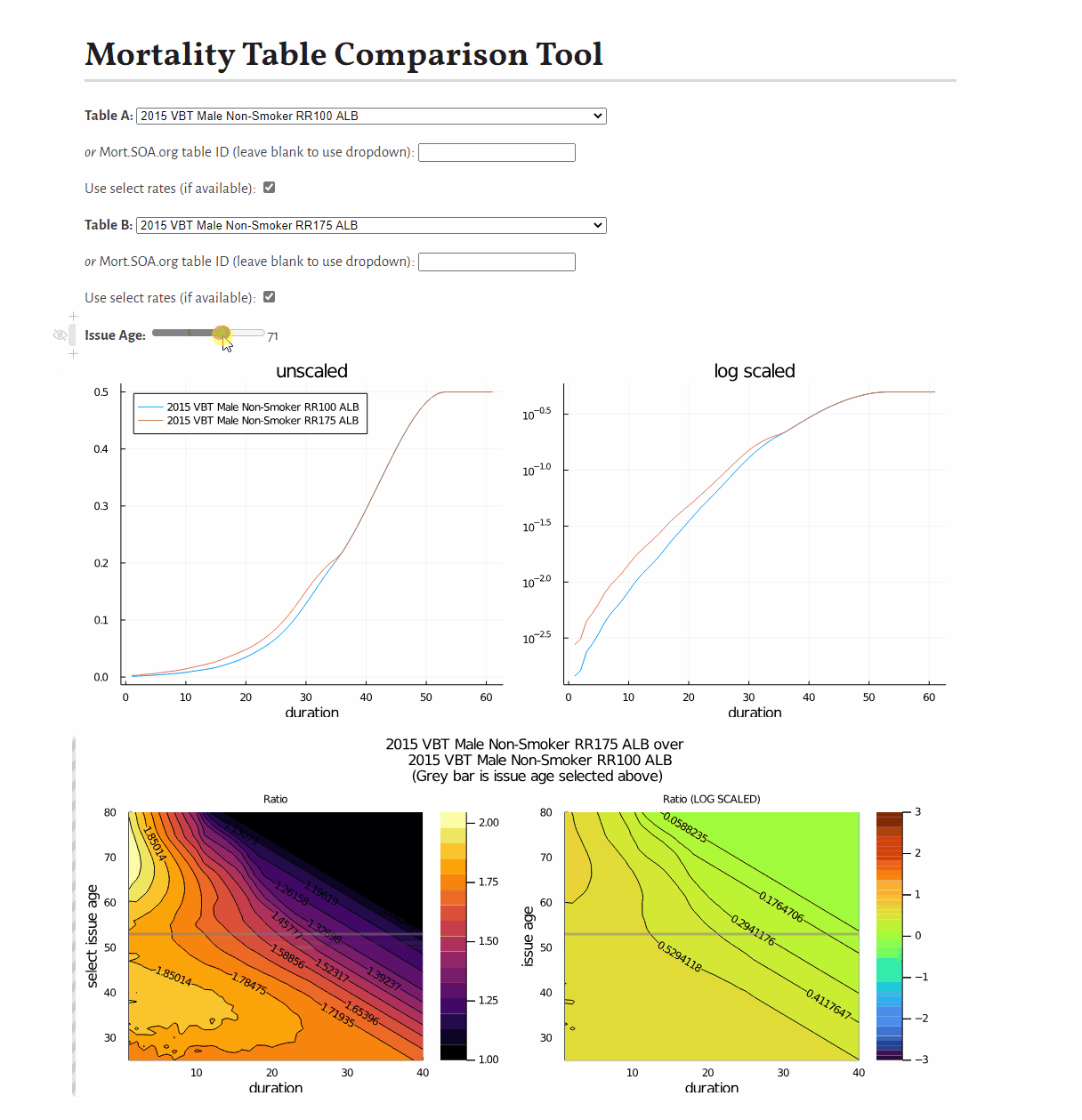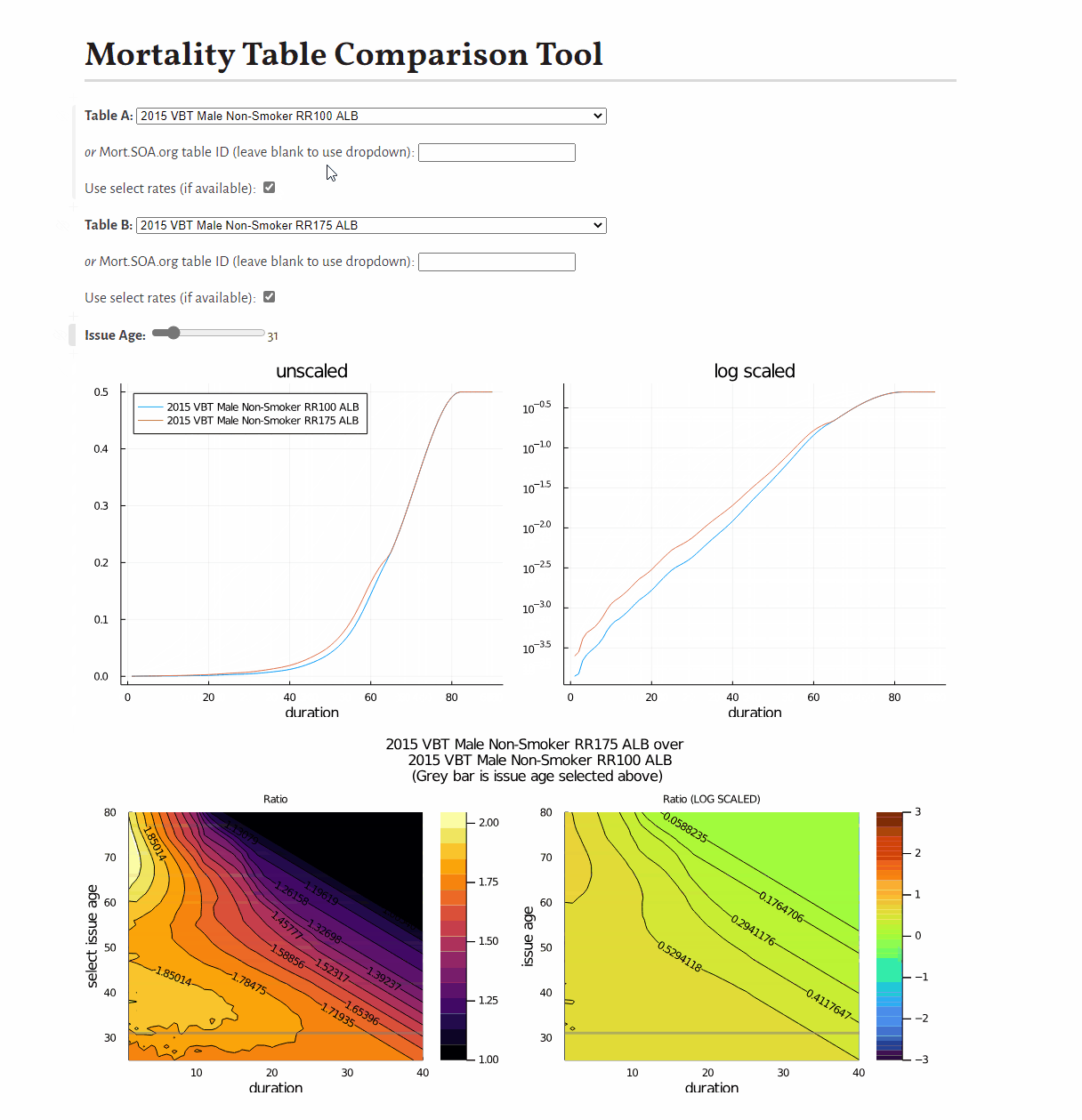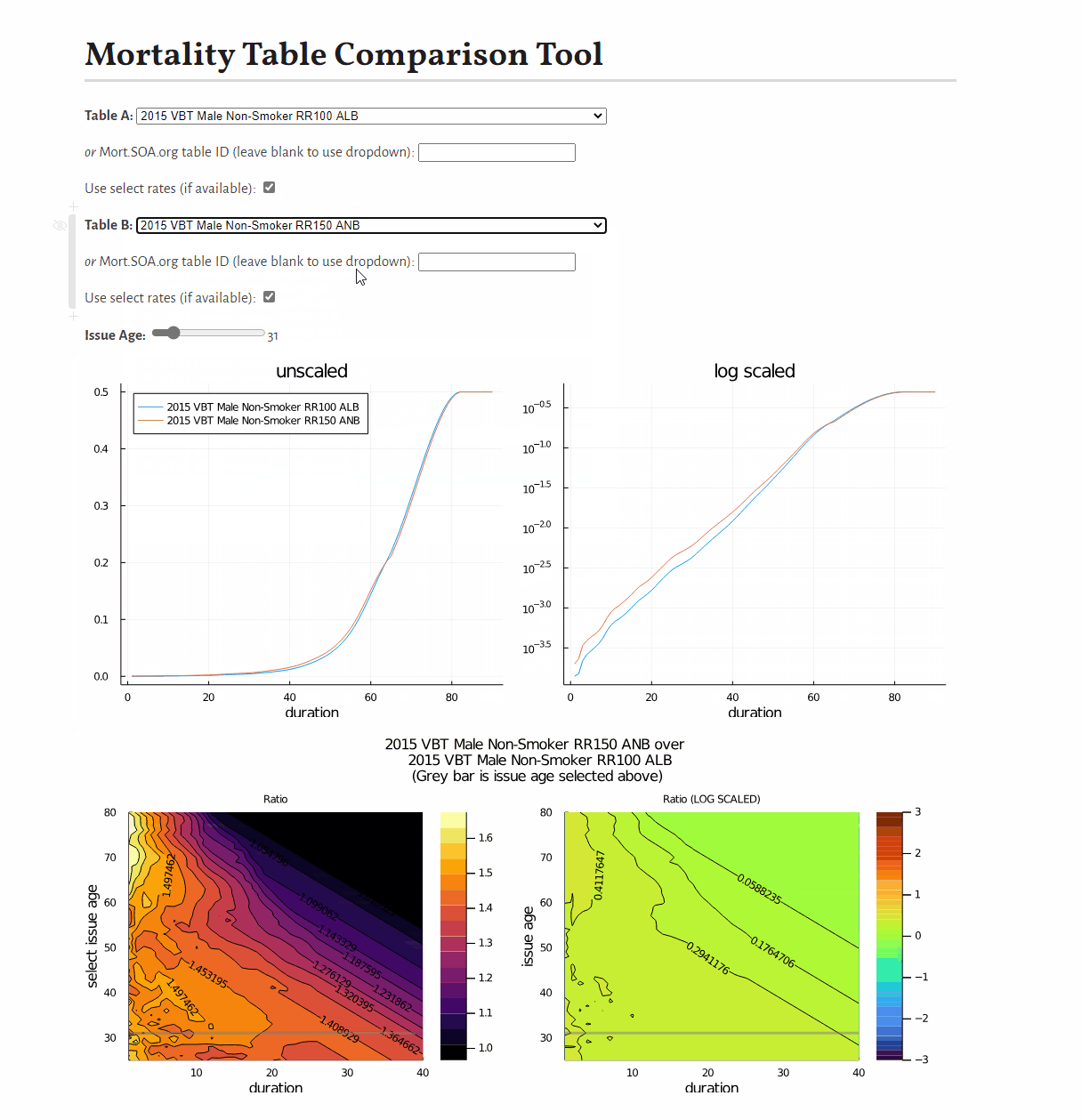
0.9887676470262408

Quickly access and compare tables

This example shows how to develop a visual comparison of rates from scratch, but you may be interested in this pre-built tool for this purpose.

using MortalityTables, Plots


cso_2001 = MortalityTables.table("2001 CSO Super Preferred Select and Ultimate - Male Nonsmoker, ANB")
cso_2017 = MortalityTables.table("2017 Loaded CSO Preferred Structure Nonsmoker Super Preferred Male ANB")

issue_age = 80
mort = [
	cso_2001.select[issue_age][issue_age:end],
	cso_2017.select[issue_age][issue_age:end],
	     ]
plot(
	   mort,
	   label = ["2001 CSO" "2017 CSO"],
	   title = "Comparison of 2107 and 2001 CSO \n for SuperPref NS 80-year-old male",
	   xlabel="duration")

Easily extend the analysis to move up the ladder of abstraction:

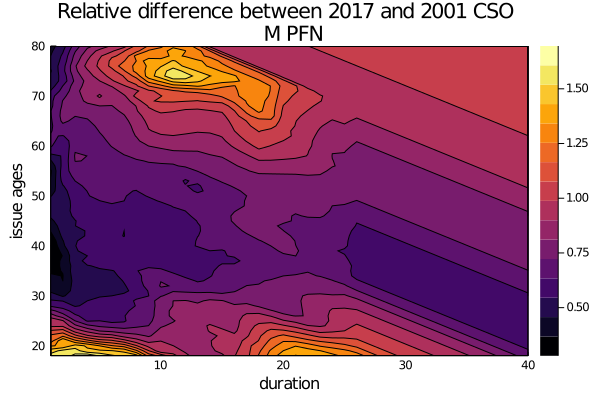
issue_ages = 18:80
durations = 1:40

# compute the relative rates with the element-wise division ("brodcasting" in Julia)
function rel_diff(a, b, issue_age,duration)
        att_age = issue_age + duration - 1
        return a[issue_age][att_age] / b[issue_age][att_age]
end


diff = [rel_diff(cso_2017.select,cso_2001.select,ia,dur) for ia in issue_ages, dur in durations]
contour(durations,
        issue_ages,
        diff,
        xlabel="duration",ylabel="issue ages",
        title="Relative difference between 2017 and 2001 CSO \n M PFN",
        fill=true
        )

Scaling and capping rates

Say that you want to take a given mortality table, scale it by 130%, and cap it at 1.0. You can do this easliy by broadcasting over the underlying rates (which is really just a vector of numbers at the end of the day):

issue_age = 30
m = cso_2001.select[issue_age]

scaled_m = min.(cso_2001.select[issue_age] .* 1.3, 1.0) # 130% and capped at 1.0 version of `m`

Note that min.(cso_2001.select .* 1.3, 1.0) won't work because cso_2001.select is still a vector-of-vectors (a vector for each issue age). You need to drill down to a given issue age or use an ulitmate table to manipulate the rates in this way.

Fractional Years

When evaluating survival over partial years when you are given full year mortality rates, you must make an assumption over how those deaths are distributed throughout the year. Three assumptions are provided as options and are based on formulas from the 2016 Experience Study Calculations paper from the SOA, specifically pages 40-44.

The three assumptions are:

• Uniform() which assumes an increasing force of mortality throughout the year.
• Constant() which assumes a level force of mortality throughout the year.
• Balducci() which assumes a decreasing force of mortality over the year. It seems to be for making it easier to calculate successive months by hand rather than any theoretical basis.

Tables

Bundled Tables

Comes with all tables built in via mort.SOA.org and by using you agree to their terms. The tables were accessed and mirrored as of the date documented in the JuliaActuary Artifacts repository

Not all tables have been tested that they work by default, though no issues have been reported with any of the the VBT/CSO/other common tables.

Load custom set of tables

Download the .xml aka the (XTbML format) version of the table from mort.SOA.org and place it in a directory of your choosing. Then call MortaliyTables.read_tables(path_to_your_dir).

mort.SOA.org Tables

Given a table id (for example 60029), you can also use this to get the table of interest:

aus_life_table_female = MortalityTables.table(60029)
aus_life_table_female[0]  # returns the attained age 0 rate of 0.10139

From CSV

If you have a CSV file that is from mort.SOA.org, or follows the same structure, then you can load and parse the table into a MortalityTable like so:

using CSV
using MortalityTables

path = "path/to/table.csv"
file = CSV.File(path,header=false) # SOA's CSV files have no true header
table = MortalityTable(file)

From XTbML

If you have a file using the XTbML format:

using MortalityTables
path = "path/to/table.xml"
table = MortalityTables.readXTbML(path)

Custom Tables

Say you have an ultimate vector and select matrix, and you want to leverage the MortalityTables package.

Here's an example, where we first construct the UlitmateMortality and then combine it with the select rates to get a SelectMortality table.

using MortalityTables

# represents attained ages of 15 through 100
ult_vec = [0.005, 0.008, ...,0.805,1.00]
ult = UltimateMortality(ult_vec,start_age = 15)

We can now use this the ultimate rates all by itself:

q(ult,15,1) # 0.005

And join with the select rates, which for our example will start at age 0:

# attained age going down the column, duration across
select_matrix = [ 0.001 0.002 ... 0.010;
                  0.002 0.003 ... 0.012;
                  ...
                ]
sel_start_age = 0
sel = SelectMortality(select_matrix,ult,start_age = 0)

sel[0][0] #issue age 0, attained age 0 rate of  0.001
sel[0][100] #issue age 0, attained age 100 rate of  1.0

Lastly, to take the SelectMortality and UltimateMortality we just created, we can combine them into one stored object, along with a TableMetaData:

my_table = MortalityTable(
              s1,
              u1,
              metadata=TableMetaData(name="My Table", comments="Rates for Product XYZ")
              )

Parameterized Models

The following parametric models are available:

Gompertz
InverseGompertz
Makeham
Opperman
Thiele
Wittstein
Perks
Weibull
InverseWeibull
VanderMaen
VanderMaen2
StrehlerMildvan
Quadratic
Beard
MakehamBeard
GammaGompertz
Siler
HeligmanPollard
HeligmanPollard2
HeligmanPollard3
HeligmanPollard4
RogersPlanck
Martinelle
Kostaki
Kannisto
KannistoMakeham

Use like so:

a = 0.0002
b = 0.13
c = 0.001
m = MortalityTables.Makeham(a=a,b=b,c=c)
g = MortalityTables.Gompertz(a=a,b=b)

Now some examples with m, but could use g interchangeably:

age = 20
m[20]                 # the mortality rate at age 20
decrement(m,20,25)    # the five year cumulative mortality rate
survival(m,20,25) # the five year survival rate

Other notes

• Because of the large number of models and the likelihood for overlap with other things (e.g. Quadratic or Weibull would be expected to be found in other contexts as well), these models Are not exported from the package, so you need to call them by prefixing with MortalityTables.
  • e.g. : MortalityTables.Kostaki()
• Because of the large number of parameters for the models, the arguments are keyword rather than positional: MortalityTables.Gompertz(a=0.01,b=0.2)
• The models have default values, so they can be called without args like this: MortalityTables.Gompertz().
  • See the help text for what the default values are: ?Gompertz

Mortality Table Comparison Tool

You may be interested in this tool to compare mortality tables:

References

• SOA Mortality Tables
• Actuarial Mathematics for Life Contingent Risks, 2nd ed
• Experience Study Calculations, SOA
• Parametric models were adapted from the MortalityLaws R package

Similar Projects

• Pyliferisk, a Python package
• Pymort, a Python package