thing is largely a work in progress
TL;DR: main notebook
There's currently many recurrent neural network architectures that utilize gates: versions of LSTM, GRU, residual RNN with forget gate, etc.
Most popular (and far from the easiest) one of them is LSTM
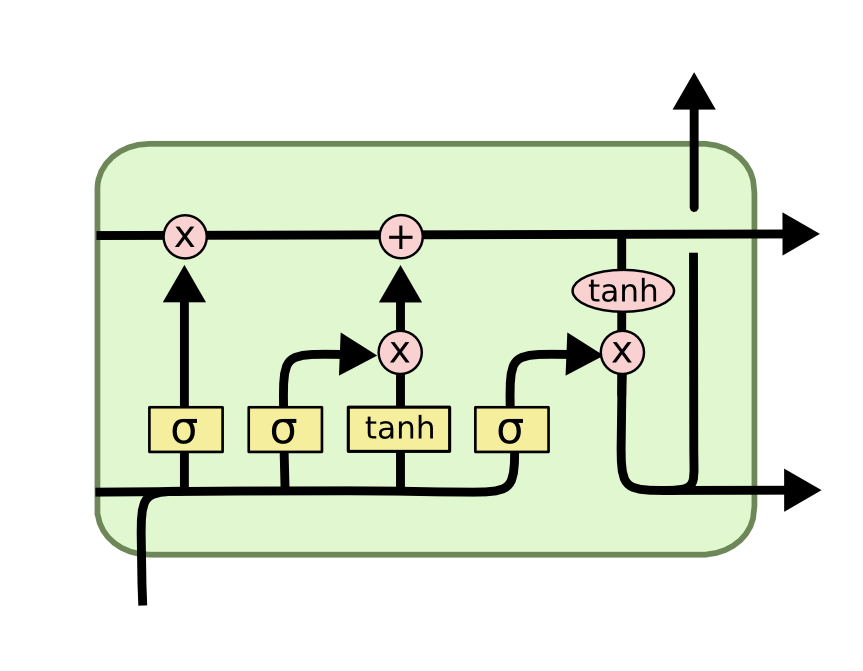
Such architectures usually take advantage of gates. For example, the LSTM above has three gates:
- input gate - network decides whether each cell (individually) is going to observe input (or ignore it)
- forget gate - network decides for each cell whether it should be kept or forgotten (set to 0)
- output gate - network decides whether a cell should be shown to other cells and to the next layer.
These gates are represented by a sigmoid of a weighted combination of input and LSTM hidden state. If you multiply e.g. cell by sigmoid in an elementwise manner, the outcome will be between 0 (if sigmoid ~ 0) and the cell itself (if sigmoid ~ 1).
In other words, the network can choose at which points of time does it wish to keep or erase the stored cell value. However, in order to train such gates with gradient descent along with the rest of the network, they have to be differentiable, thus necessarily continuous.
Thus, network is able to e.g. multiply one of it's stored cell values by 0.7324 by producing such value out of forgetgate sigmoid. This may be useful in some cases, but most of the time forgetgate is meant to be either 0 or 1.
There has recently been a trick that allows train networks with quasi-discrete categorical activations via gumbel-softmax or gumbel-sigmoid nonlinearity. A great explaination of how it works can be found here.
The trick is to add a special noize to the softmax distribution that favors almost-1-hot outcomes. Such noize can be obtained from gumbel distribution. Since sigmoid can be viewed as a special case of softmax of 2 classes(logit and 0), we can use the same technique to implement an LSTM network with gates that will ultimately be forced to converge to 0 or 1. Here's a demo of gumbel-sigmoid on a toy task.
Such network can then be binarized: multiplication can be replaced with if/else operations and fp16 operations to drastically improve execution speed, especially when implemented in a special-purpose device, see here and here.
- moar experiments
- moar gated architectures
- multilayer stuff
- other temperature regimes
- converting pretrained rnn to binary
- Lambda Lab
- Arseniy Ashukha (advice & useful comments)