📌 질문은 zzsza님의 Datascience-Interview-Questions를 참고하였습니다.
- 알고 있는 metric에 대해 설명해주세요. (ex. RMSE, MAE, recall, precision ...)
- 정규화를 왜 해야할까요? 정규화의 방법은 무엇이 있나요?
- Local Minima와 Global Minima에 대해 설명해주세요.
- 차원의 저주에 대해 설명해주세요.
- dimension reduction 기법으로 보통 어떤 것들이 있나요?
- PCA는 차원 축소 기법이면서, 데이터 압축 기법이기도 하고, 노이즈 제거기법이기도 합니다. 왜 그런지 설명해주실 수 있나요?
- LSA, LDA, SVD 등의 약자들이 어떤 뜻이고 서로 어떤 관계를 가지는지 설명할 수 있나요?
- Markov Chain을 고등학생에게 설명하려면 어떤 방식이 제일 좋을까요?
- 텍스트 더미에서 주제를 추출해야 합니다. 어떤 방식으로 접근해 나가시겠나요?
- SVM은 왜 반대로 차원을 확장시키는 방식으로 동작할까요? SVM은 왜 좋을까요?
- 다른 좋은 머신 러닝 대비, 오래된 기법인 나이브 베이즈(naive bayes)의 장점을 옹호해보세요.
- 회귀 / 분류시 알맞은 metric은 무엇일까?
- Association Rule의 Support, Confidence, Lift에 대해 설명해주세요.
- 최적화 기법중 Newton’s Method와 Gradient Descent 방법에 대해 알고 있나요?
- 머신러닝(machine)적 접근방법과 통계(statistics)적 접근방법의 둘간에 차이에 대한 견해가 있나요?
- 인공신경망(deep learning이전의 전통적인)이 가지는 일반적인 문제점은 무엇일까요?
- 지금 나오고 있는 deep learning 계열의 혁신의 근간은 무엇이라고 생각하시나요?
- ROC 커브에 대해 설명해주실 수 있으신가요?
- 여러분이 서버를 100대 가지고 있습니다. 이때 인공신경망보다 Random Forest를 써야하는 이유는 뭘까요?
- K-means의 대표적 의미론적 단점은 무엇인가요? (계산량 많다는것 말고)
- L1, L2 정규화에 대해 설명해주세요.
- Cross Validation은 무엇이고 어떻게 해야하나요?
- XGBoost을 아시나요? 왜 이 모델이 캐글에서 유명할까요?
- 앙상블 방법엔 어떤 것들이 있나요?
- feature vector란 무엇일까요?
- 좋은 모델의 정의는 무엇일까요?
- 50개의 작은 의사결정 나무는 큰 의사결정 나무보다 괜찮을까요? 왜 그렇게 생각하나요?
- 스팸 필터에 로지스틱 리그레션을 많이 사용하는 이유는 무엇일까요?
- OLS(ordinary least squre) regression의 공식은 무엇인가요?
평가지표(metric)을 크게 분류를 위한 평가지표와 회귀를 위한 평가지표로 나눌 수 있다.
우선 분류 작업(task)에 적용할 수 있는 평가지표를 살펴보자.
정확도(accuracy)
정확도는 모델의 예측이 얼마나 정확한지를 의미한다. 정확도는 (예측 결과가 동일한 데이터 개수)/(전체 예측 데이터 개수)로 계산할 수 있다. 하지만 라벨 불균형이 있는 데이터에서 정확도를 사용하면 안 된다. 예를 들면, 0과 1의 비율이 9:1인 데이터가 있다고 했을 때, 모두 0으로 예측하면 정확도가 90%가 나올 것이다. 이는 잘못된 판단이므로 정확한 판단을 위해서는 다른 지표를 사용해야 한다.
오차 행렬(confusion matrix)
오차 행렬은 모델이 예측을 하면서 얼마나 헷갈리고 있는지를 보여주는 지표이다. 주로 이진 분류에서 많이 사용하며 이진 분류에 대한 오차 행렬은 위의 그림처럼 같이 나타낼 수 있다. True Positive는 긍정으로 예측을 했는데 실제로 긍정인 경우를, False Positive는 긍정으로 예측했는데 실제로 부정인 경우를, False Negative는 부정으로 예측했는데 실제로 긍정인 경우를, True Negative는 부정으로 예측했는데 실제로 부정인 경우를 말한다. 위의 값을 바탕으로 모델이 어떤 오류를 발생시켰는지를 살펴볼 수 있다.
참고로 정확도는 (TN + TP) / (TN + FP + FN + TP)로 계산할 수 있다.
정밀도(precision), 재현율(recall)
정밀도와 재현율은 긍정 데이터 예측 성능에 초점을 맞춘 평가지표이다. 정밀도란 예측을 긍정으로 한 데이터 중 실제로 긍정인 비율을 말하며, 재현율은 실제로 긍정인 데이터 중 긍정으로 예측한 비율을 말한다. 오차 행렬을 기준으로 정밀도는 TP / (FP + TP)으로, 재현율은 TP / (FN + TP)으로 계산할 수 있다.
정밀도와 재현율은 트레이드오프 관계를 갖는다. 정밀도는 FP를, 재현율은 FN을 낮춤으로써 긍정 예측의 성능을 높인다. 이 같은 특성 때문에 정밀도가 높아지면 재현율은 낮아지고 재현율이 높아지면 정밀도는 낮아진다. 가장 좋은 경우는 두 지표 다 적절히 높은 경우이다.
F1-Score
정밀도와 재현율 한 쪽에 치우치지 않고 둘 다 균형을 이루는 것을 나타낸 것이 F1-Score이다. F1-Score는 정밀도와 재현율의 조화평균으로 계산할 수 있다.
ROC-AUC
ROC는 FPR(False Positive Rate)가 변할 때 TPR(True Positive Rate)가 어떻게 변하는지를 나타내는 곡선을 말한다. 여기서 FPR이란 FP / (FP + TN)이고, TPR은 TP / (FN + TP)으로 재현율을 말한다. 그럼 어떻게 FPR을 움직일까? 바로 분류 결정 임계값을 변경함으로써 움직일 수 있다. FPR이 0이 되려면 임계값을 1로 설정하면 된다. 그럼 긍정의 기준이 높으니 모두 부정으로 예측될 것이다. 반대로 1이 되려면 임계값을 0으로 설정하여 모두 긍정으로 예측시키면 된다. 이렇게 임계값을 움직이면서 나오는 FPR과 TPR을 각각 x와 y 좌표로 두고 그린 곡선이 ROC이다.
AUC는 ROC 곡선의 넓이를 말한다. AUC가 높을수록 즉, AUC가 왼쪽 위로 휘어질수록 좋은 성능이 나온다고 판단한다. 즉, TPR이 높고 FPR이 낮을수록 예측 오류는 낮아지기 때문에 성능이 잘 나온다 볼 수 있다.
마지막으로 회귀 작업에 적용할 수 있는 평가지표를 살펴보자.
MAE(Mean Absolute Error)는 예측값과 정답값 사이의 차이의 절대값의 평균을 말한다.
MSE(Mean Squared Error)는 예측값과 정답값 사이의 차이의 제곱의 평균을 말하며, MAE와 달리 제곱을 했기 때문에 이상치에 민감하다.
RMSE(Root Mean Squared Error)는 MSE에 루트를 씌운 값을 말한다.
RMSLE(Root Mean Squared Logarithmic Error)는 RMSE와 비슷하나 예측값과 정답값에 각각 로그를 씌워 계산을 한다.
R Squared는 분산을 기반으로 예측 성능을 평가하는 지표를 말한다. 정답값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 정확도가 높다.
- 14 Popular Machine Learning Evaluation Metrics - RUBIK'S CODE
- Metrics to Evaluate your Machine Learning Algorithm - towards data science
- 머신러닝 용어집 - 구글 머신러닝 단기 집중과정
- 3. 평가 - 파이썬 머신러닝 완벽 가이드
- Regression 모델 평가 : MSE, MAE, RMSE, RMSLE, R-Squared - Steadiness
정규화는 개별 피처의 크기를 모두 똑같은 단위로 변경하는 것을 말한다. 정규화를 하는 이유는 피처의 스케일이 심하게 차이가 나는 경우 값이 큰 피처가 더 중요하게 여겨질 수 있기 때문이다. 이를 막기 위해 피처 모두 동일한 스케일로 반영되도록 하는 것이 정규화이다.
정규화하는 방법으로는 대표적으로 두 가지가 존재한다. 첫 번째 정규화 방법은 최소-최대 정규화(min-max normalization)으로 각 피처의 최소값을 0, 최대값을 1로 두고 변환하는 방법이다. 값을
비용 함수(cost function)에서의 Global Minima는 에러가 최소화되는 즉, 우리가 찾고자 하는 지점을 말하며, Local Minima는 에러가 최소가 될 수 있는 후보가 되는 지점 중 Global Minima를 뺀 지점을 말한다. Local Minima는 자칫 에러가 최소화되는 지점을 찾았다고 착각할 수 있기에 함정에 비유할 수 있다. 이를 해결하기 위해 Momentum과 같은 최적화 알고리즘을 사용하거나 학습률(learning rate)를 잘 조절하여 Local Minima에서 벗어날 수 있다.
차원의 저주란 데이터 차원이 증가할수록 해당 공간의 크기가 기하급수적으로 증가하여 데이터 간 거리가 기하급수적으로 멀어지고 희소한 구조를 갖게 되는 현상을 말한다. 이를 해결하기 위해서는 차원을 증가시킨만큼 더 많은 데이터를 추가하거나 PCA, LDA, LLE, MDS와 같은 차원 축소 알고리즘으로 차원을 줄여 해결할 수 있다.
차원 축소는 피처 선택(feature selection)과 피처 추출(feature extraction)으로 나눌 수 있다. 우선 피처 선택은 특정 피처에 종속성이 강한 불필요한 피처는 제거하고 데이터의 특징을 잘 표현하는 주요 피처만 선택하는 것을 말한다. 반면 피처 추출은 기존 피처를 저차원의 피처로 압축하여, 피처를 함축적으로 잘 설명할 수 있도록 저차원으로 매핑하는 것을 말한다. 대표적인 피처 추출 알고리즘으로 PCA, SVD, NMF, LDA 등이 있다.
PCA(Principle Component Analysis)는 입력 데이터의 공분산 행렬을 기반으로 고유벡터를 생성하고 이렇게 구한 고유 벡터에 입력 데이터를 선형 변환하여 차원을 축소하는 방법이다. 차원은 곧 입력 데이터의 피처를 뜻하므로 데이터 압축 기법으로 볼 수도 있다.
또한 PCA는 고유값이 가장 큰, 즉 데이터의 분산이 가장 큰 순으로 주성분 벡터를 추출하는데, 가장 나중에 뽑힌 벡터보다 가장 먼저 뽑힌 벡터가 데이터를 더 잘 설명할 수 있기 때문에 노이즈 제거 기법이라고도 불린다.
PCA는 Principle Component Analysis의 약자로 데이터의 공분산 행렬을 기반으로 고유벡터를 생성하고 이렇게 구한 고유 벡터에 입력 데이터를 선형 변환하여 차원을 축소하는 방법이다. SVD는 Singular Value Decomposition의 약자로 PCA와 유사한 행렬 분해 기법을 사용하나 정방 행렬(square matrix)를 분해하는 PCA와 달리 행과 열의 크기가 다른 행렬에도 적용할 수 있다.
LSA는 Latent Semantic Analysis의 약자로 잠재 의미 분석을 말하며, 주로 토픽 모델링에 자주 사용되는 기법이다. LSA는 DTM(Document-Term Matrix)이나 TF-IDF(Term Frequency-Inverse Document Frequency) 행렬에 Truncated SVD를 적용하여 차원을 축소시키고, 단어들의 잠재적인 의미를 이끌어낸다. Truncated SVD는 SVD와 똑같으나 상위 n개의 특이값만 사용하는 축소 방법이다. 이 방법을 쓸 경우 원 행렬로 복원할 수 없다.
LDA는 Latent Dirichlet Allocation 혹은 Linear Discriminant Analysis의 약자이다. 전자는 토픽모델링에 사용되는 기법 중 하나로 LSA와는 달리 단어가 특정 토픽에 존재할 확률과 문서에 특정 토픽이 존재할 확률을 결합확률로 추정하여 토픽을 추정하는 기법을 말한다. 후자는 차원축소기법 중 하나로 분류하기 쉽도록 클래스 간 분산을 최대화하고 클래스 내부의 분산은 최소화하는 방식을 말한다.
Latent Dirichlet Allocation와 관련된 자세한 내용은 #9 텍스트 더미에서 주제를 추출해야 합니다. 어떤 방식으로 접근해 나가시겠나요?을 참고해주세요!
- 잠재 의미 분석(Latent Semantic Analysis, LSA) - 딥러닝을 이용한 자연어 처리 입문
- 잠재 디리클레 할당(Latent Dirichlet Allocation, LDA) - 딥러닝을 이용한 자연어 처리 입문
- 문서 단어 행렬(Document-Term Matrix, DTM) - 딥러닝을 이용한 자연어 처리 입문
- TF-IDF(Term Frequency-Inverse Document Frequency) - 딥러닝을 이용한 자연어 처리 입문
- 6. 차원 축소 - 파이썬 머신러닝 완벽 가이드
마코프 체인(Markov Chain)
마코프 체인이란 마코프 성질을 지닌 이산 확률 과정(Discrete-time Stochastic Pross)을 말한다.
마코프 성질(Markov Property)
정리하면 마코프 체인은 확률변수(random variable)가 어떤 상태(state)에 도달할 확률이 오직 바로 이전 시점의 상태(state)에 달려 있는 경우를 가리킨다.
예를 들어, 오늘의 날씨가 어제의 날씨에만 의존하면 1차 마코프 체인, 이틀 전까지의 날씨에만 의존하면 2차 마코프 체인이다.
마코프 모델(Markov Model)
마코프 모델은 위의 가정하에 확률적 모델을 만든 것으로써 가장 먼저 각 상태를 정의하게 된다. 상태(state)는
그리고 상태와 상태 전이 확률을 정리하여 상태 전이도(state transition diagram)으로도 표현할 수 있다.
- Markov Chain - MLWiki
- [기술면접] Markov Chain, Gibbs Sampling, 마르코프 체인, 깁스 샘플링 (day2 / 201010) - huidea
- (Bayes 학습)(4)마르코프 연쇄-(1) - 정보사회학연구소
잠재 디리클레 할당(Latent Dirichlet Allocation, LDA)
잠재 디리클레 할당(LDA)이란 문서의 집합에서 토픽을 찾아내는 프로세스를 뜻하는 토픽 모델링의 대표적인 알고리즘을 말한다. LDA는 "문서들은 토픽들의 혼합으로 구성되어져 있으며, 토픽들은 확률 분포에 기반하여 단어들을 생성한다"고 가정하며, 데이터가 주어지면 LDA는 토픽을 문서가 생성되던 과정을 역추적한다.
예를 들어, 다음과 같은 예시 문장 3개가 있다고 가정하자.
문서1 : 저는 사과랑 바나나를 먹어요
문서2 : 우리는 귀여운 강아지가 좋아요
문서3 : 저의 깜찍하고 귀여운 강아지가 바나나를 먹어요
LDA를 통해 각 문서의 토픽 분포와 각 토픽 내의 단어 분포를 추정할 수 있다.
- 각 문서의 토픽 분포
- 문서1 : 토픽 A 100%
- 문서2 : 토픽 B 100%
- 문서3 : 토픽 B 60%, 토픽 A 40%
- 각 토픽의 단어 분포
- 토픽A : 사과 20%, 바나나 40%, 먹어요 40%, 귀여운 0%, 강아지 0%, 깜찍하고 0%, 좋아요 0%
- 토픽B : 사과 0%, 바나나 0%, 먹어요 0%, 귀여운 33%, 강아지 33%, 깜찍하고 16%, 좋아요 16%
LDA는 토픽의 제목을 정해주지 않지만, 이 시점에서 알고리즘의 사용자는 위 결과로부터 두 토픽이 각각 과일에 대한 토픽과 강아지에 대한 토픽이라고 판단해볼 수 있다.
SVM(Support Vector Machine)은 데이터가 사상된 공간에서 경계로 표현되며, 공간상에 존재하는 여러 경계 중 가장 큰 폭을 가진 경계를 찾는다.
-
$$B_1$$ : 결정 경계 -
$$b_{11}$$ : plus-plane -
$$b_{12}$$ : minus-plane
SVM의 장단점은 다음과 같다.
| 장점 | 단점 |
|---|---|
| 분류와 회귀에 모두 사용할 수 있다. | 데이터 전처리와 매개변수 설정에 따라 정확도가 달라질 수 있다. |
| 신경망 기법에 비해 과적합 정도가 낮다. | 예측이 어떻게 이루어지는지에 대한 이해와 모델에 대한 해석이 어렵다. |
| 예측의 정확도가 높다. | 대용량 데이터에 대한 모델 구축 시 속도가 느리며,메모리 할당량이 크다. |
| 저차원과 고차원 데이터에 대해서 모두 잘 작동한다. |
마진(Margin)
마진(Margin)은 plus-plane과 minus-plane 사이의 거리를 의미하며, 최적의 결정 경계는 마진을 최대화한다.
SVM은 선형 분류뿐만 아니라 비선형 분류에도 사용되는데, 비선형 분류에서는 입력자료를 다차원 공간상으로 맵핑할 때 커널 트릭(kernel trick)을 사용하기도 한다. 원공간(Input Space)의 데이터를 선형분류가 가능한 고차원 공간(Feature Space)으로 매핑한 뒤 두 범주를 분류하는 초평면을 찾는다. (Kernel-SVM)
커널 트릭(Kernel Trick)
커널 함수를 이용하여 차원 공간(low dimensional space)을 고차원 공간(high dimensional space)으로 매핑해주는 작업을 커널트릭이라 한다.
커널 함수의 종류는 다음과 같다.
- 서포트 벡터 머신 (Support Vector Machine) - ratsgo's blog
- Kernel-SVM - ratsgo's blog
- Support Vector Machine (SVM)의 개념 - butter_shower
- Support Vector Machine (SVM, 서포트 벡터 머신) - Excelsior-JH
- 서포트 벡터 머신(Support Vector Machine) 쉽게 이해하기 - 아무튼 워라벨
- ADP 필기 올패키지 데이터 분석 전문가
데이터에서 변수들에 대한 조건부 독립을 가정하는 알고리즘으로 클래스에 대한 사전 정보와 데이터로부터 추출된 정보를 결합하고, 베이즈 정리(Bayes Theorem)를 이용하여 어떤 데이터가 특정 클래스에 속하는지 분류하는 알고리즘이다.
나이브 베이즈의 장단점은 다음과 같다.
| 장점 | 단점 |
|---|---|
| 단순하고 빠르며 매우 효과적이다 | 모든 속성은 동등하게 중요하고 독립적이라는 알려진 결함 가정에 의존한다 |
| 노이즈와 결측 데이터가 있어도 잘 수행한다 | 수치 속성으로 구성된 많은 데이터셋에 대해 이상적이지 않다 |
| 훈련에 대한 상대적으로 적은 예제가 필요하지만 매우 많은 예제도 잘 수행한다 | 추정된 확률은 예측된 범주보다 덜 신뢰적이다 |
| 예측에 대한 추정된 확률을 얻기 쉽다 |
- 쉽고 강력한 머신러닝, 나이브 베이즈 분류 (Naive Bayes Classification)- 자비스가 필요해
- 나이브 베이즈 알고리즘의 장점과 단점 - 웹개발공작소
- ADP 필기 올패키지 데이터 분석 전문가
#1 답변을 참고해주세요. 해당 답변에서 서술하지 않은 지표만 추가로 설명합니다.
회귀
결정계수(Coefficient of determination)는 (회귀선에 의해 설명되는 변동)/(전체 변동)을 말하며, 독립변수의 개수가 많아질수록 결정계수가 1에 가까워진다. 회귀모형이 높은 결정계수를 갖는다면 실제로 모형이 설명력이 높은 것인지 단순히 독립변수의 개수가 많은 것인지 알기 어려워 결정계수를 신뢰할 수 없게 되는 문제가 발생한다.
수정된 결정계수는 결정계수의 문제를 해결하기 위해 표본의 크기(n)와 독립변수의 수(p)를 고려하여 수정된 결정계수를 계산한다.
분류
$$
- (y - \log (p))) + (1 - y) \log (1-p) $$
Log Loss 혹은 Binary Crossentropy는 이진 분류에서의 지표로 사용된다.
Categorical Crossentropy는 분류해야할 클래스가 3개 이상인 멀티 클래스 분류에서의 지표로 사용된다.
- 상관계수 & 결정계수 & 수정된 결정계수 - 모찌의 맛집 통계
- [결정계수] R square와 adjusted R square - specialscene
- 3 Best metrics to evaluate Regression Model?
- The 5 Classification Evaluation metrics every Data Scientist must know
연관규칙분석(Association Analysis)은 흔히 장바구니 분석(Market Basket Analysis) 또는 서열분석(Sequence Analysis)이라고 불린다. 기업의 데이터베이스에서 상품의 구매, 서비스 등 일련의 거래 또는 사건들 간의 규칙을 발견하기 위해 적용하며, 연관성 분석의 평가 지표로는 Support, Confidence, Lift를 사용한다.
Support(지지도)
전체 거래 중 항목 A와 항목 B를 동시에 포함하는 거래의 비율로 정의한다.
Confidence(신뢰도)
항목 A를 포함한 거래 중에서 항목 A와 항목 B가 같이 포함될 확률이다. 연관성의 정도를 파악할 수 있다.
Lift(향상도)
A가 구매되지 않았을 때 품목 B의 구매확률에 비해 A가 구매됐을 때 품목 B의 구매확률의 증가 비이다. 연관규칙 A→B는 품목 A와 품목 B의 구매가 서로 관련이 없는 경우에 향상도가 1이 된다.
에를 들어 어떤 슈퍼마켓에서 5명의 고객에 의해 발생된 5(
| Customer ID |
Transaction ID |
Items |
|---|---|---|
| 1131 | no.1 | 계란, 우유 |
| 2094 | no.2 | 계란, 기저귀, 맥주, 사과 |
| 4122 | no.3 | 우유, 기저귀, 맥주, 콜라 |
| 4811 | no.4 | 계란, 우유, 맥주, 기저귀 |
| 8091 | no.5 | 계란, 우유, 맥주, 콜라 |
- 지지도(Support) =
$$s(X→Y) = \frac{n(X\cup Y)}{N} = \frac{n\left{no.2, no.4\right}}{N} = \frac{2}{5} = 0.4$$ - 신뢰도(Confidence) =
$$c(X→Y) = \frac{n(X\cup Y)}{n(X)} = \frac{n\left{no.2, no.4\right}}{n\left{no.2, no.4, no.5\right}} = \frac{2}{3} = 0.6667$$ - 향상도(Lift) =
$$Lift(X→Y) = \frac{c(X→Y)}{s(Y)} = \frac{0.6667}{0.6} = 1.1111$$
- [R 연관규칙(Association Rule)] 지지도(support), 신뢰도(confidence), 향상도(lift), IS측도, 교차지지도 - R, Python 분석과 프로그래밍의 친구 (by R Friend)
- ADP 필기 올패키지 데이터 분석 전문가
Newton's Method
함수
여기서
이
Gradient Descent
Gradient descent에서는 함수
Newton’s method와 동일하게 위 근사식의 gradient가 0인
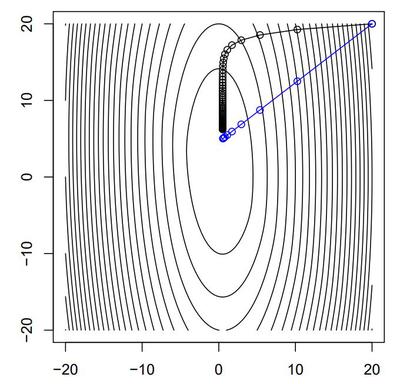
Newton's method와 Gradient descent의 step에 따른 수렴 방향 비교
- 파랑: Newton's method
- 검정: Gradient descent
Gradient descent는 2차 미분항을 정방행렬에 상수가 곱해진 값으로 가정하고 gradient를 계산하기 때문에, 등고선(contour)의 접선 방향에 수직하게(perpendicular) 수렴함을 확인할 수 있고, Newton’s method에 비해 느린 수렴 속도를 보인다.
- 14-01-01 Newton's method interpretation - 모두를 위한 컨벡스 최적화
- 뉴턴법/뉴턴-랩슨법의 이해와 활용(Newton's method) - 다크 프로그래머
- Gradient Descent 탐색 방법 - 다크 프로그래머
- 4주차_#2. 최적화 기법중 Newton's Method와 Gradient Descent 방법을 설명하세요. - 내가 보려고 만든 공간
머신러닝적 접근방법과 통계적 접근방법의 차이는 두 방법의 주 목적이 다르다는 것이다.
머신러닝적 접근방법은 모델의 예측 성공률을 높이는게 목적이다.
따라서 모델의 신뢰도나 정교한 가정보다는 다양한 피쳐를 사용하여 (오버피팅을 감안하더라도) 높은 예측률을 달성하고자 한다.
통계적 접근방법은 분포와 가정을 통해 신뢰 가능하고 정교한 모델을 만드는게 목적이다.
따라서 모형을 복잡하지 않고 단순하게 만들고, 어떤 피쳐가 어떤 원인을 주는지 알 수 있도록 한다.
딥러닝 이전의 인공신경망은 선형적으로만 회귀, 분류를 수행하기 때문에 레이어를 깊게 쌓지 못했고, 때문에 XOR 문제 같은 복잡한 문제를 풀지 못하는 문제점이 있었다.
하지만 시그모이드와 같은 비선형 함수를 선형 모델에 추가하여 XOR 문제를 해결하고, 편미분 체인룰을 사용한 오차역전파 방법으로 모델을 업데이트할 수 있게 되면서 레이어를 깊게 쌓은 딥러닝 인공신경망이 발전하였다.
ImageNet 과 같은 거대하고 높은 품질의 데이터셋이 모두에게 공개되면서 딥러닝의 혁신적인 발전이 시작될 수 있었다. 현재는 더 다양한 태스크에 적합한 좋은 GLUE 같은 데이터들도 공개되어 더욱 딥러닝의 발전에 이바지하고 있다.
현재 좋은 성능을 내는 딥러닝 모델들은 모두 큰 규모의 모델들인데 하드웨어의 발전이 이를 가능하게 하였다.
또한 end-to-end 모델이 나타나면서 데이터 레이블링, 하이퍼파라미터 찾기, 최적 모델 찾기 등 모든 작업을 기계에게 맡기면서 딥러닝이 크게 발전하였다.
ROC 커브는 이진분류 모델의 성능을 나타내는 지표이다.
모델이 참이라고 예측하는 경우는 FPR (False Positive Rate, 실제 값이 거짓일 때) 과 TPR (True Positive Rate, 실제 값이 참일 때) 두 경우로 나뉜다.
FPR 과 TPR 을 그래프에서 x 축, y 축으로 동시에 표현한 ROC 커브를 통해 모델이 얼마나 옳은 값을 잘 예측하는지 알 수 있게 된다.
ROC 커브가 좌상단과 가까운 경우 좋은 모델이라고 판단할 수 있다. 모델이 FPR 은 낮게, TPR 은 높게 예측하기 때문이다.
랜덤 포레스트는 여러 결정 트리를 앙상블하여 하나의 모델로 구성하는 방법이다. 랜덤 포레스트에서는 각 서버를 모델의 특성을 이해하는 단일 결정 트리 (Decision tree) 로 병렬적이게 구성할 수 있다.
반면, 인공신경망은 하나의 서버 자체가 모델의 특성을 모두 이해하는 end-to-end 구조로 직렬적이게 구성된다.
따라서 서버가 100대 있을 때는, 이를 병렬적으로 활용할 수 있는 랜덤 포레스트를 사용한다.
- Random Forest(랜덤 포레스트) 개념 정리 - Codesigner's Dev Story
- 의사결정나무 - ratsgo's blog
- 출근 루틴, 하루 3문제 - Man-About-Town
K-means 는 특성이 비슷한 데이터를 같은 그룹으로 묶어주는 클러스터링 알고리즘으로, k 개의 군집 개수를 정하고 군집의 중심점을 예측하여 각 데이터와 거리를 비교한 후 군집을 결정한다.
K-means 알고리즘의 단점은 다음과 같다.
- K 를 몇 개로 설정하냐에 따라 성능이 달라진다.
- K 개 군집의 중심점을 예측하여야 하는데, 어디를 중심점으로 두냐에 따라 성능이 달라진다.
- 데이터가 잘 모여있는 경우에 효과적이지, 노이즈가 많은 경우 효과적이지 않다.
정규화(일반화)의 목적은 모델이 학습 데이터에 오버피팅되지 않고 처음 보는 테스트 데이터에도 좋은 성능을 내도록 만드는 것이다.
모델의 학습은 loss 함수를 최소화하는 방향으로 진행된다.
이 때, loss 함수에 L1, L2 정규화 항 (norm) 을 더함으로써 모델은 기존의 loss 도 줄이면서 정규화 항 (모델의 피쳐값과 관련) 도 줄이는 방향으로 학습된다.
모델의 피쳐값이 줄어듦에 따라 특정 피쳐가 너무 큰 값을 갖지 않게 되면서 오버피팅을 방지할 수 있게 된다.
L1 정규화 (라쏘 회귀)
L1 정규화는 특정 피쳐의 값이 매우 낮은 경우 (아웃라이어) 0에 수렴되는 특징이 있다. 특정 피쳐가 0이 되어 사라지는 것은 feature selection 과 동일하다고 볼 수 있다.
L2 정규화 (릿지 회귀)
L2 정규화는 특정 웨이트의 값이 매우 낮아도 0에 수렴되지는 않고 가까워지는 특징이 있다. 이는 L1 정규화에 비해 강하지 않게 정규화를 실행하여 항상 선형 모델에 일반화 효과를 줄 수 있다.
loss 식에 람다 모델의 웨이트에 대한 L1 or L2 norm 을 더해줌으로써 모델의 일반화가 가능해진다.
loss 는 데이터 값과 추정 값의 차이로 모델은 loss 를 최소화하는 방향으로 학습하는데, L1 or L2 정규화를 사용하면 loss 가 웨이트의 크기만큼 커지기 때문에 데이터 값에 예측 값이 fit 해지지 않기 때문이다.
Norm
Norm은 벡터의 크기를 나타내는 것으로 L1 Norm은 벡터의 절댓값 크기를 나타내고, L2 Norm은 직선 거리 (제곱의 루트) 를 나타낸다.
위 그림에서 초록선은 L2 norm 을 의미하고, 나머지 선은 L1 norm 을 의미한다.
- L1 loss
- L2 loss
- 딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명 - 빛나는 나무
- L1, L2 Norm, Loss, Regularization? - 생각 정리
- 릿지회귀, 라쏘회귀, 엘라스틱넷 - 대학원생이 쉽게 설명해보기
cross validation(교차검증)이란 train(학습) 데이터로 학습한 모델이, 학습에 사용되지 않은 validation(검증) 데이터를 기준으로 얼마나 잘 동작하는지 확인하는 것이다. 여기서 주의할 점은 train 데이터셋과 validation 데이터셋에는 test 데이터셋이 포함되면 안된다는 것이다.
교차검증을 통해 얻을 수 있는 장단점은 아래와 같다.
- 적은 데이터에 대한 validation 신뢰성을 높일 수 있다.
- 모든 데이터셋을 훈련에 활용할 수 있으므로 데이터 편중을 막을 수 있다. (k-fold 경우)
- 검증 결과에 따라 더 일반화된 모델을 만들 수 있다.
- 모델 학습에 오랜 시간이 소요된다.
교차검증 기법의 종류는 아래와 같다. (validation 데이터셋을 어떻게 지정하느냐에 따라 달라진다.)
- 홀드 아웃 교차검증(Holdout Cross Validation)
- K-겹 교차검증(K-fold Cross Validation)
- 계층별 k-겹 교차검증(Stratified K-Fold Cross Validation)
홀드 아웃 교차검증
홀드아웃 교차검증방법은 일정한 비율의 validation 데이터셋 하나를 지정하여 검증 데이터셋으로 사용하는 것이다. 홀드아웃 교차검증을 사용하는 경우, 두가지 문제점이 존재한다.
- validation 데이터셋으로 지정된 부분의 데이터가 학습셋으로 사용되지 않는다는 문제
- validation 데이터셋에 편향되도록 모델을 조정하게 된다는 문제
이를 해결하기 위해 k-겹 교차검증이 등장했다.
k-겹 교차검증
k-겹 교차검증 방법은 train 데이터를 k개의 fold로 나누어, 그 중 하나의 fold를 validation 데이터셋으로 삼아 검증하는 방법을 k번 반복하여, 그 평균을 결과로서 사용하는 방법이다. 세부적인 동작방법은 다음과 같다.
- train 데이터셋을 k개의 fold로 나누고, 그 중 하나를 validation 데이터셋으로 지정한다.
- validation 데이터셋을 제외한 나머지 폴드들을 train 데이터셋으로 사용하여 모델을 학습한다.
- 학습한 모델을 1번에서 지정해둔 validation 데이터셋으로 검증하고, 그 검증 결과를 저장해둔다.
- 모델을 초기화한 후, 기존 validation 데이터셋이 아닌 다른 fold를 validation 데이터셋으로 지정하고, 2번 과정부터 다시 수행한다.
- 모든 fold들이 한번씩 validation 데이터셋으로 사용된 후에는, 저장해둔 검증결과의 평균을 내어, 그것을 최종 validation 결과로 사용한다.
그러나 k-겹 교차검증 방법은 랜덤하게 validation 데이터셋을 지정하게 되므로, 편향된 데이터로 이뤄진 폴드가 생성될 수 있다는 단점이 있다. 이를 해결하기 위해서 계층별 k-겹 교차검증 방법이 등장했다.
계층별 k-겹 교차검증
계층별 k-겹 교차검증 방법은 k-겹 교차검증 방법에서 fold를 나눌때, 랜덤하게 fold를 지정하는 것이 아닌, 각 클래스별 비율을 고려하여 fold를 구성하는 방법이다.
💡 왜 test 데이터셋 만으로 검증하면 안될까?
모든 train 데이터셋을 학습하고, test 데이터셋으로 검증한 결과를 확인한다고 하자. 개발자는 test 데이터셋 점수를 높이기 위해, test 데이터셋에 편향되도록 모델을 튜닝하게 될 것이다. 그러나 중요한 것은 test 데이터셋에 대한 정확도를 높이는 것 뿐만아니라, 모델의 일반적인 정확도를 높이는 것이다. 어떤 데이터가 들어와도 일정하게 높은 정확도를 보여주는 모델이 좋은 모델이라 할 수 있으므로, validation 데이터셋과 test 데이터셋을 분리하여 검증하는 과정을 통해, 모델을 일반화시켜야 한다.
XGBoost(eXtreme Gradient Boosting) 이란, 트리 기반의 앙상블 학습에서 가장 각광받고 있는 알고리즘 중 하나이다. Kaggle 경연대회에서 상위를 차지한 많은 과학자들이 XGBoost를 이용하면서 널리 알려졌다. GBM에 기반하고 있지만, GBM의 단점인 느린 수행시간 및 과적합 규제(Regularization) 부재 등의 문제를 해결해서 각광받고 있다.
XGBoost의 장점은 다음과 같다.
- 분류와 회귀영역에서 뛰어난 예측 성능을 발휘한다.
- XGBoost는 병렬처리를 사용하여, GBM 대비 빠른 수행시간을 보인다.
- Regularization, Early Stopping 기능을 통해 오버피팅을 방지할 수 있다.
- Tree Pruning(가지치기) 제공한다. 미리 정해둔 max_depth까지만 split하고 pruning을 하고, 거꾸로 올라가면서 positive gain이 없는 노드를 삭제한다.
- 자체적으로 결측치를 처리해준다.
- 매 iteration마다 교차검증을 수행한다.
GBM(Gradient Boosting Algorithm) 이란 회귀분석 또는 분류 분석을 수행할 수 있는 예측모형이며 예측모형의 앙상블 방법론 중 부스팅 계열에 속하는 알고리즘이다. LightGBM, CatBoost, XGBoost는 모두 GBM을 기반으로 만들어졌다. (자세한 내용은 Gradient Boosting Algorithm의 직관적인 이해 - DeepPlay 참고)
💡 boosting 이라는 테크닉 자체가 sequential 한데 어떻게 병렬처리를 할까?
세가지 가능성이 제기된다. 나뉜 분기마다 각각 병렬처리하거나, 분기가 나뉘는 지점 계산을 병렬처리 하거나, 처음부터 feature별 정렬을 통해 병렬처리를 할 수 있다. (자세한 내용은 XGBoost의 병렬처리가 어떻게 가능할까? - GoLab 참고)
앙상블(Ensemble) 은 여러개의 모델을 조합해서 그 결과를 뽑아 내는 방법이다. "정확도가 높은 강한 모델을 하나 사용하는 것보다, 정확도가 낮은 약한 모델을 여러개 조합 하는 방식의 정확도가 높다"는 개념에서 비롯한 방법이다. Bagging, Boosting, Stacking 등의 방법이 있다.
배깅(Bagging, Bootstrap Aggregation) 이란 샘플을 여러번 뽑아(Bootstrap = 복원 랜덤 샘플링) 각 모델을 학습시켜 결과물을 집계(Aggregation)하는 방법이다. 카테고리 데이터는 투표 방식(Votinig)으로 결과를 집계하며, 연속형 데이터는 평균으로 집계한다. Bagging을 사용한 대표적인 기법에는 Random Forest 방법이 있다. 학습 데이터가 충분하지 않더라도 충분한 학습효과를 주어 높은 bias의 underfitting 문제나, 높은 variance로 인한 overfitting 문제를 해결하는데 도움을 준다.
부스팅(Boosting) 이란 이전 모델의 오답에 가중치를 높게 부여하여 다음 모델을 학습하는 방법이다. 오답을 정답으로 맞추기 위해 오답에 더 집중하여 학습시키기 떄문에 일반적으로 배깅에 비해 정확도가 높다. 그러나 틀렸던 부분에 대해 반복적으로 학습하므로 오버피팅의 문제가 있으며, outlier에 취약하고, 속도가 느리다는 단점도 가지고 있다. GBM(Gradient Boosting) 방법이 대표적이고, XGBoost, AdaBoost, GradientBoost 등의 알고리즘이 존재한다.
스태킹(Stacking) 이란 여러 개별 모델이 예측한 결과값을 다시 학습 데이터셋으로 사용해서 모델을 만드는 방법이다. 그러나 위의 그림과 같은 기본적인 스태킹 방법은 같은 데이터셋을 통해 예측한 결과를 기반으로 다시 학습하므로 오버피팅 문제점이 있다. 따라서 스태킹에 Cross Validation 방식을 도입하여 이 문제를 해결할 수 있다. 데이터를 쪼개고 이들 중 일부만을 가지고 학습한 모델을 여러개 만들어, 그 결과들을 메타 학습 데이터셋(meta train dataset) 으로 사용하여 다시 학습하는 것이다. 이 방법은 많은 개별 모델의 결과를 결합하여 예측 성능을 높일 수 있다는 장점이 있다.
💡 배깅 vs 부스팅
배깅은 랜덤 복원추출(부트스트랩)을 여러번 반복하여 모델을 병렬적으로 여러개 학습을 시킨 다음, 평균을 내는 방식이다. 반면, 부스팅은 모든 데이터를 학습에 사용하되, 오답에 더 큰 가중치를 두어 다음 회차를 학습시키는 순차적인 방법이다.
특징(feature) 이란, 샘플(데이터)을 잘 설명하는 측정가능한 속성이다. 특징을 통해 특정 샘플을 수치화하여 나타낼 수 있다.
특징벡터(feature vector) 란 피쳐(feature)들의 집합이다. 굳이 벡터로 표시하는 이유는 수학적으로 다루기 편하기 때문이다.
데이터별로 어떤 특징을 가지고 있는지 찾아내고, 그것을 토대로 데이터를 벡터로 변환하는 작업을 특징추출(feature extraction) 이라고 한다.
특징 공간(feature space) 이란 관측값들이 있는 공간을 의미한다. 이 특징 공간은 여러 차원으로 구성될 수 있다. 어떤 데이터를 특징공간의 하나의 벡터로 표현하는 경우, 여러 특징 변수가 특징벡터에 영향을 줄 수 있다. 예를들어, 특징 변수가 하나인 데이터는 1차원 특징 공간에 나타나고, 특징 변수가 N개라면 N차원의 특징 공간에 나타낼 수 있다.
d-차원 데이터의 특징 벡터는 다음과 같이 표시된다.
💡 분야에 따른 피처벡터의 의미
- 컴퓨터비전(이미지)에서의 특징은 edge, corner 등을 의미한다. 픽셀 값이 급격히 변화하는 곳, 밝기의 변화, 색상의 변화, 그래디언트의 방향 등의 매칭 정보등을 특징으로 삼는다. SIFT, SURF 등의 방법이 존재한다.
- 자연어처리(텍스트) 에서의 특징은 단어, 형태소, 서브워드, 토큰 등으로 표현될 수 있으며, BOW(Bag-of-Words)는 문서에서 단어의 발생을 설명하는 텍스트의 벡터 표현이다. 만약 8개의 단어로 이루어진 문장을 BoW로 만들면, 8차원(dimension)의 vector로서 하나의 단어를 표현할 수 있다.
- 정형데이터에서의 특징은 각 attribute(열)를 의미한다. 키, 나이, 국적 등이 특징으로 사용될 수 있다.
- 피쳐(기계학습) - 위키백과
- 4)머신러닝이란? - TCPschool.com
- 머신러닝-다차원 특징공간과 차원의 저주 - 예비 개발자
- OpenCV-특징검출, 디스크립터, 매칭 - JeongYongHwang
- 자연어처리 Bag of Words
- 자연어의 피처와 전처리 - GeumjaeLee
한 줄로 요약하자면, 좋은 모델은 데이터의 패턴을 잘 학습한 모델로서, 한번도 본적 없는 데이터에 대해 옳은 판단을 내리는 모델이 좋은 모델이라고 할 수 있다.
머신러닝, 딥러닝 등을 사용하여 모델을 생성하는 이유는 기계가 사람 대신 어떠한 결정을 내리기 위함이다. 따라서 모델은 결정을 대신하는 기계, 결정기라고 볼 수 있다.
이 관점에서, 좋은 결정(옳은 결정)을 내리는 모델이 좋은 모델이다. 주어진 학습 데이터에 과적합된 모델의 경우, 주어진 데이터와 조금만 다른 데이터가 들어오면 제대로 분류하지 못하는 상황이 발생된다.
그러므로 모델의 일반화가 이루어져, 새로운 데이터에 대해서도 적정한 수준의 성능을 보이는 모델이 좋은 모델이라고 할 수 있다.
예를들어, 예측이 목적이라면, 실제 정답과 예측 값의 차이(loss, cost, error)를 최소화 하는 모델이 가장 좋은 모델이다. 또한 확률을 추정하는 경우에는 가능성(likelihood)을 최대화하는 모델이 좋은 모델이라고 할 수 있다.
50개의 작은 의사결정 나무는 앙상블에서 Bagging 기법을 사용한 모델로 볼 수 있다. 따라서 Bagging의 대표적인 방법인 Random Forest 방법이 왜 좋은지 설명하는 것으로, 왜 50개의 작은 의사결정 나무가 더 나은지 설명하고자 한다.
큰 트리는 작은 편향(bias)와 큰 분산(variance)를 갖기 때문에, 매우 깊이 성장한 트리는 훈련데이터에 대해 과적합(overfitting)하게 된다. Random Forest 방식으로 학습하면, 트리들의 편향은 그대로 유지하면서, 여러 데이터셋/여러 경우에 대해 학습하기 떄문에 분산을 감소시킬 수 있다. 또한 한 개의 결정트리의 경우, train 데이터에 있는 노이즈에 대해 매우 민감하지만, 여러 트리들을 만들면서 평균을 내면, 노이즈에 대해 강인해질 수 있다. 따라서 하나의 깊은/큰 의사결정 나무보다 50개의 작은 의사결정 나무가 더 좋은 모델을 완성시킨다고 할 수 있다.
Bagging(Bootstrap Aggregating)
Bagging은 Bootstrap(반복, 복원추출)하고, 이를 Aggregation(집계)하는 방법이다. 원래 데이터셋에 대해서 여러개의 작은 데이터셋 N개를 샘플링해서 만든다음, 각각의 데이터를 작은 모델 N개로 학습을 시킨다. 그 다음 학습된 N개의 모델을 모두 하나로 합쳐서 최종적인 모델로 사용하는 방법론을 의미한다. 결국, 병렬적으로 데이터를 나누어 여러 개의 모델을 동시에 학습시키는 방법이다.
Random Forest
Random Forest는 여러 의사 결정 나무를 생성한 후에 다수결(hard voting) 또는 평균(soft voting)에 따라 출력을 예측하는 알고리즘이다. 즉 의사 결정 나무와 bagging을 혼합한 형태라고 볼 수 있다. Random Forest의 특징은 bootstrap을 이용하여 학습 데이터셋에서 다양한 샘플을 추출하여 일부만 한번의 학습에 사용한다는 것이다. 데이터 샘플링 및 변수 선택을 통해 의사 결정 나무의 다양성을 확보할 수 있다. 이를 통해 예측의 변동성이 줄어들고, 과적합을 방지할 수 있어 결측치에 대해 강건하다는 장점을 가진다. 그러나 데이터의 수가 많아지면 의사결정나무에 비해 속도가 크게 떨어지고, 결과에 대한 해석이 어렵다는 단점이 있다.
- Bagging, Boosting, Bootstrapping - 곽동현, New Sight
- Bagging(Bootstrap aggregating, 배깅)알고리즘 - InCastle
- 머신러닝: Random Forest 특징, 개념, 장점, 단점
스팸 필터는 메일이 스팸 메일인지 아닌지에 대한 확률을 계산하여, 메일을 분류(Classification) 하는 문제이다. 로지스틱 회귀는 회귀를 바탕으로 데이터가 어떤 범주에 속할 확률을 0과 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류(Classification)해주는 지도 학습 알고리즘이다. 특히 입력값이 아무리 크거나 작아도 0에서 1 사이의 값으로 맵핑시킨다는 점에서 분류문제에 적합하다. 따라서 로지스틱 회귀가 스팸필터에 많이 사용된다.
분류문제에서 로지스틱 회귀가 적절한 이유
로지스틱 회귀는 시그모이드 함수(sigmoid function) 를 통해 선형함수를 0과 1 사이의 함수로 바꾼 것이며, S자 형태를 보인다. 시그모이드 함수의 정의는 아래와 같다.
로지스틱 회귀의 가설함수는 다음과 같다.
x값이 아무리 +, -로 작아지거나 커져도 항상 0과 1 사이의 값을 반환한다. 확률은 0에서 1사이의 범위 내에 들어와야하므로 이러한 형태가 적합하다.
이렇게 H(x)의 값이 0과 1사이로 나오면, 위의 Hypothesis 함수로 regression을 한 결과값이 threshold(ex.0.5) 이상인 경우엔 1로 분류하고, threshold 보다 작으면 0으로 분류하면 되기 떄문이다.
분류문제에서 선형회귀가 적합하지 않은 이유
그림1과 같이 주어진 데이터를 표현하는 그래프를 그려, 적절한 지점을 기준으로 두 그룹으로 분류할 수 있다.
이때 그림2의 new 데이터가 새로 들어왔다고 해보자. 그래프는 새로운 데이터 new의 영향을 받아, 아래로 기울어진 형태로 업데이트되어, 그림3의 붉은색 그래프 형태가 된다.
이렇게 되면, 원래는 1로 잘 분류되던 것들의 예측값이 기존 threshold 아래로 내려가게되어, 0으로 분류되어버리는 문제가 발생한다.
선형회귀 함수는 어떤 입력값이 들어오느냐에 따라 0과 1 사이의 범위를 벗어나기도 한다.
또한, H(x) = 100x라는 가설함수(Hypothesis function)이 있다고 하자. x가 0.01 이상인 경우는 모두 1로 x가 0 이하인 경우는 모두 0으로 분류하게 된다. 이처럼 x값에 너무 민감하게 반응하는 모델이 만들어질 수 있다. 연산상으로는 매우 작은 값만 바뀌어도 아예 분류자체가 바뀌어버린다.
더 나아가, 선형모델은 확률이 아닌, 점들의 보간(interpolate)만으로 이루어지므로 확률로 해석할 수 없다. 예측값이 확률이 아니기 때문에 한 클래스와 다른 클래스를 구분할 수 있는 의미 있는 임계값이 없다. 또한 다중 클래스를 가지는 분류문제로 확장할 수 없다는 문제점도 있다. 이러한 문제점들 때문에, 분류문제에서 선형 회귀 모델은 적합하지 못하다.
- 4.2 Logistic Regression - TooTouch
- 5)로지스틱회귀 - 딥러닝을 이용한 자연어 처리 입문
- 모두를 위한 딥러닝(sung kim)lec5-Logistic Classification - cdjs의 코딩 공부방
최소자승법(OLS, Ordinary Least Squares) 이란, 산점도를 통해 데이터의 분포 그래프를 그릴때, 이 데이터들의 경향을 알기 위한 최적의 추세선을 그리기 위한 방법 중 하나이다. OLS는 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법이다.
OLS Regression은 회귀를 통해서 방정식의 상수 값들을 추정하는 데에 사용된다. n개의 입력값과 그에 대응하는 출력값
추정하고자 하는 파라미터 β에 대한 표현식을 다음과 같이 구할 수 있다.
$$ {\hat {\beta}}=(\mathbf {X} ^{\rm {T}}\mathbf {X})^{-1}\mathbf {X}^{\rm {T}}\mathbf {y} ={\big (},{\textstyle \sum }\mathbf {x} _{i}\mathbf {x} _{i}^{\rm {T}},{\big )}^{-1}{\big (},{\textstyle \sum }\mathbf {x} {i}y{i},{\big)} $$
예를들어, 7개 데이터의 경향을 나타내는 추세선을 그림2와 같이 그렸다고 하자.
이때 실제 데이터의 y값(실제값)과 추세선의 y값(예측값)의 차를 잔차(Residual) 라고 한다. (아래 그래프에서 잔차는 점선으로 표시)
최소자승법은 이 잔차의 제곱의 합(RSS, Residual Sum of Squares)을 최소로 하는 (가중치 벡터를 구하는) 방법이다.
잔차 제곱의 합은 그림3의 TOTAL AREA에 해당하는 넓이와 같다.
잔차 제곱의 합을 구하는 식은 아래와 같다.
파란색 추세선보다 보라색 추세선의 잔차제곱의 합이 더 작다. 따라서 파란색 추세선보다 보라색 추세선이 위 7개의 데이터를 더 잘 표현해주는 추세선임을 알 수 있다. 이렇게 잔차 제곱의 합을 최소로 하는 방법이 최소자승법이며, 최소자승법을 활용하여 데이터를 가장 잘 표현하는 선형 회귀선을 그릴 수 있다.
💡 OLS vs. MSE
- OLS(Ordinary Least Square): 선형 회귀 모델을 만들기 위한 선횡 최소 제곱법, 모델을 만들때 사용한다.
- MSE(Mean Square Error): 모델 성능 평가 지표, 모델을 평가할 때 사용한다.