-
Notifications
You must be signed in to change notification settings - Fork 644
腾讯&字节等:最小的k个数 #59
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Comments
var newsort = arr.sort((a, b) => a - b)
return newsort.slice(0, k)
function quicksort(arr) {
if(arr.length <= 1) return arr
var pivotIndex = Math.floor(arr.length / 2)
var pivot = arr.splice(pivotIndex, 1)[0];
var left = []
var right = []
for(let i=0; i < arr.length; i++) {
if(arr[i] < pivot) {
left.push(arr[i])
} else {
right.push(arr[i])
}
}
return quicksort(left).concat(pivot, quicksort(right))
} |
简单粗暴排序+ 先把输入的 /**
* @param {number[]} arr
* @param {number} k
* @return {number[]}
*/
const getLeastNumbers = function(arr, k) {
arr.sort((a, b) => a - b)
return arr.slice(0, k)
};但是这样的时间复杂度是 快排快排的 关键 在于先在数组中选择一个数字,接下来把数组中的数字分为两部分,比选择的数字小的数字移到数组的左边,比选择的数字大的数字移到数组的右边。这个函数可以这样实现 function partition (arr, low, high) {
let x = arr[high];
let i = low - 1;
for(let j = low; j < high; j++) {
if(arr[j] <= x){
i++;
[arr[i], arr[j]] = [arr[j], arr[i]]
}
}
[arr[i+1], arr[high]] = [arr[high], arr[i+1]]
return i + 1;
}比第 /**
* @param {number[]} arr
* @param {number} k
* @return {number[]}
*/
const getLeastNumbers = function(arr, k) {
const length = arr.length;
if (k >= length) return arr;
let left = 0,
right = length - 1;
let index = partition(arr, left, right);
while (index !== k) {
if (index < k) {
left = index + 1;
index = partition(arr, left, right);
} else if (index > k) {
right = index - 1;
index = partition(arr, left, right);
}
}
return arr.slice(0, k);
};时间复杂度为 备注:看了一早上这种方法的实现,脑子不够用了。附本人觉得的优秀答案解答 |
|
排序加获取 function quicksort(arr) {
if (arr.length <= 1) return arr;
const pivotIndex = Math.floor(arr.length / 2);
const pivot = arr.splice(pivotIndex, 1)[0];
const left = [];
const right = [];
for (let i = 0; i < arr.length; i++) {
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quicksort(left).concat(pivot, quicksort(right));
}
function findK(arr, k) {
return quicksort(arr).slice(0, k);
} |
|
这是一道典型的 Top k 问题
这种问题我们该怎么处理喃? 最简单的就是将数组进行排序(可以是最简单的快排),取前 K 个数就可以了,so easy 解答一:数组排序,取前 k 个数代码实现: let getLeastNumbers = function(arr, k) {
return arr.sort((a, b) => a - b).slice(0, k);
}复杂度分析:
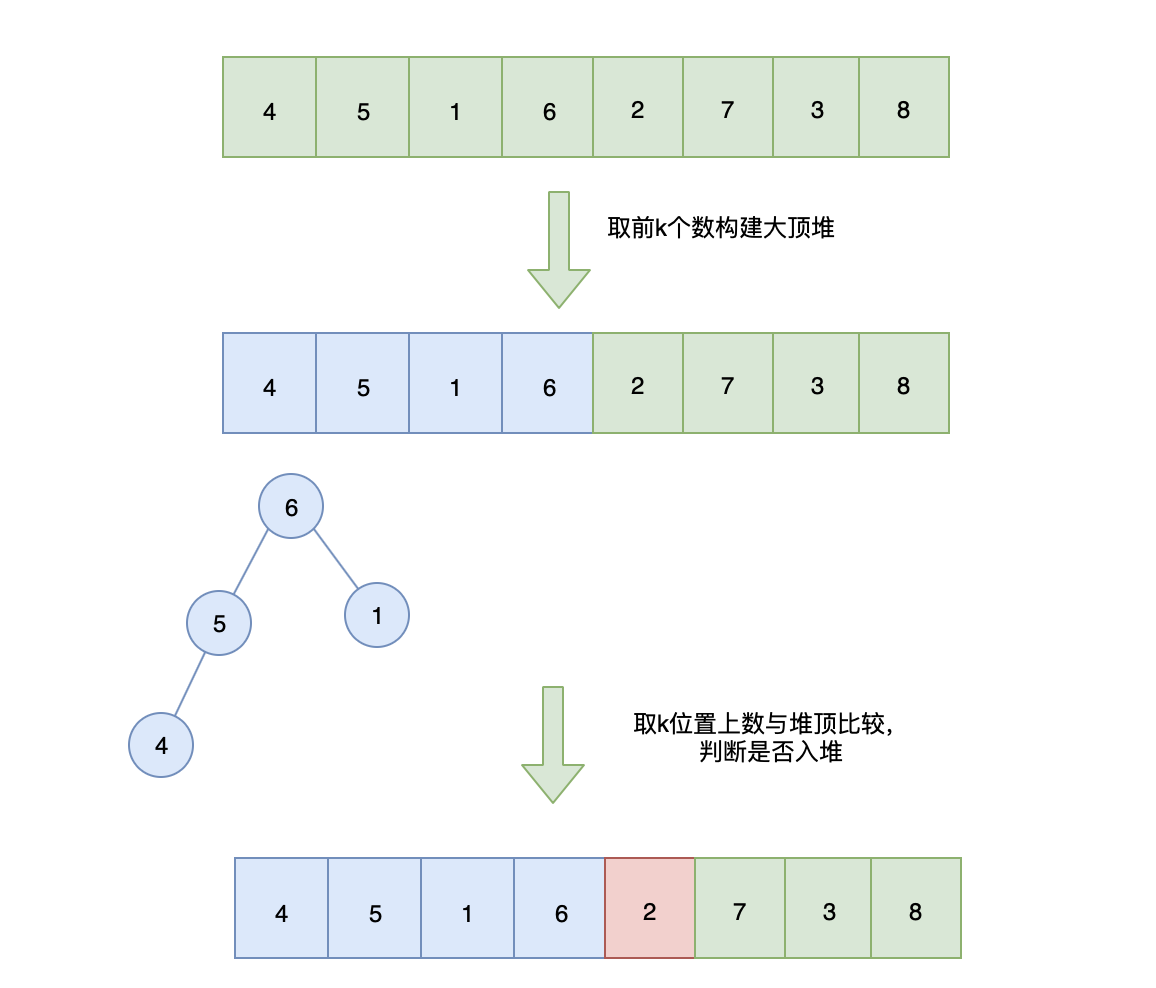
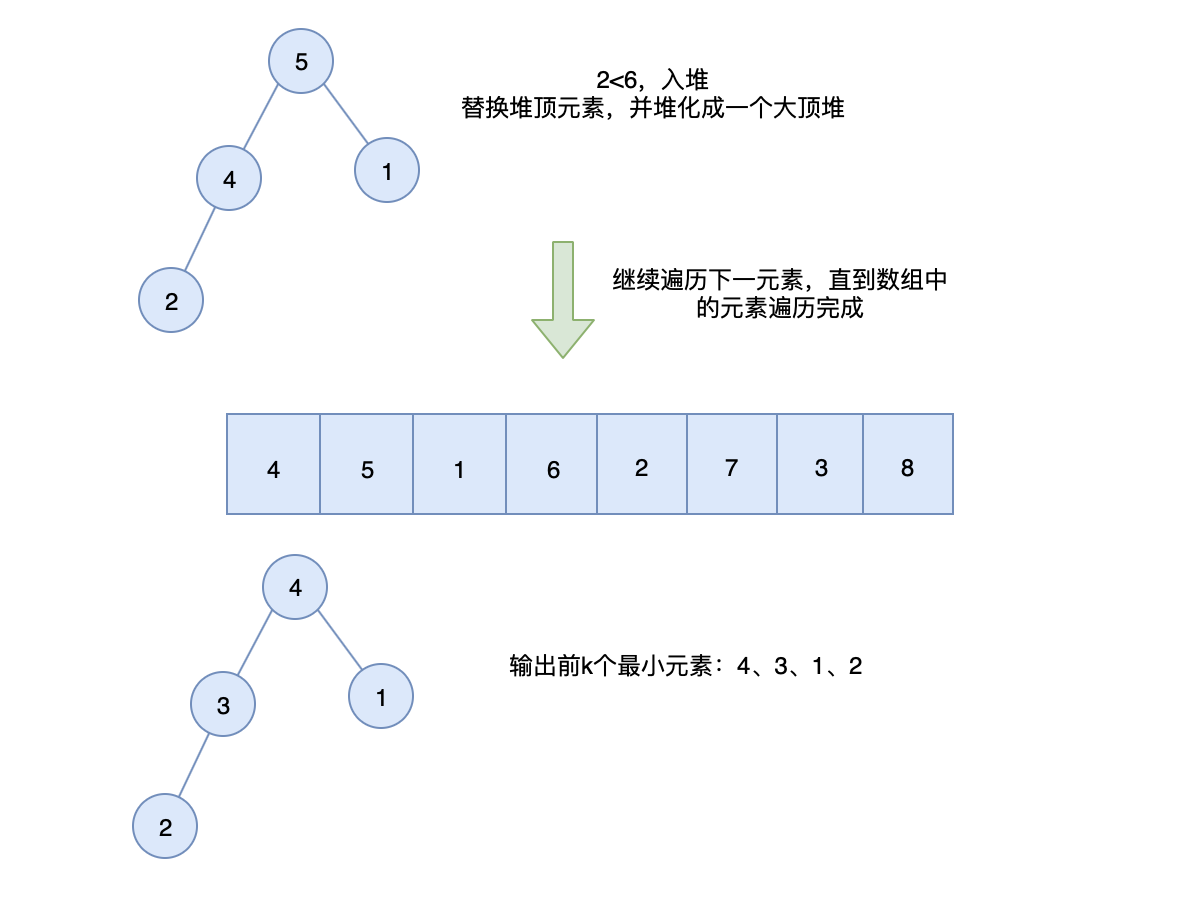
注意: 在 V8 引擎 7.0 版本之前,数组长度小于10时, 在 V8 引擎 7.0 版本之后就舍弃了快速排序,因为它不是稳定的排序算法,在最坏情况下,时间复杂度会降级到 O(n2)。 而是采用了一种混合排序的算法:TimSort 。 这种功能算法最初用于Python语言中,严格地说它不属于以上10种排序算法中的任何一种,属于一种混合排序算法: 在数据量小的子数组中使用插入排序,然后再使用归并排序将有序的子数组进行合并排序,时间复杂度为 解法二:构建大顶堆求 Top k问题我们也可以通过构造一个大顶堆来解决,大顶堆上的任意节点值都必须大于等于其左右子节点值,即堆顶是最大值。 所以我们可以重数组中取出 具体步骤如下:
代码实现: let getLeastNumbers = function(arr, k) {
// 从 arr 中取出前 k 个数,构建一个大顶堆
let heap = [,], i = 0
while(i < k) {
heap.push(arr[i++])
}
buildHeap(heap, k)
// 从 k 位开始遍历数组
for(let i = k; i < arr.length; i++) {
if(heap[1] > arr[i]) {
// 替换并堆化
heap[1] = arr[i]
heapify(heap, k, 1)
}
}
// 删除heap中第一个元素
heap.shift()
return heap
};
// 原地建堆,从后往前,自上而下式建大顶堆
let buildHeap = (arr, k) => {
if(k === 1) return
// 从最后一个非叶子节点开始,自上而下式堆化
for(let i = Math.floor(k/2); i>=1 ; i--) {
heapify(arr, k, i)
}
}
// 堆化
let heapify = (arr, k, i) => {
// 自上而下式堆化
while(true) {
let maxIndex = i
if(2*i <= k && arr[2*i] > arr[i]) {
maxIndex = 2*i
}
if(2*i+1 <= k && arr[2*i+1] > arr[maxIndex]) {
maxIndex = 2*i+1
}
if(maxIndex !== i) {
swap(arr, i, maxIndex)
i = maxIndex
} else {
break
}
}
}
// 交换
let swap = (arr, i , j) => {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}复杂度分析:
利用堆求 Top k 问题的优势这种求 Top k 问题是可以使用排序来处理,但当我们需要在一个动态数组中求 Top k 元素怎么办喃? 动态数组可能会插入或删除元素,难道我们每次求 Top k 问题的时候都需要对数组进行重新排序吗?那每次的时间复杂度都为 O(nlogn) 这里就可以使用堆,我们可以维护一个 K 大小的小顶堆,当有数据被添加到数组中时,就将它与堆顶元素比较,如果比堆顶元素大,则将这个元素替换掉堆顶元素,然后再堆化成一个小顶堆;如果比堆顶元素小,则不做处理。这样,每次求 Top k 问题的时间复杂度仅为 O(logk) 更多堆内容可查看 前端进阶算法9:看完这篇,再也不怕堆排序、Top K、中位数问题面试了 解法三:计数排序计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。它是一种典型的拿空间换时间的排序算法 代码实现: let getLeastNumbers = function(arr, k) {
return countingSort(arr, 10000, k)
}
let countingSort = (arr, maxValue, k) => {
// 开辟的新的数组,用于将输入的数据值转化为键存储
var bucket = new Array(maxValue + 1),
sortedIndex = 0,
arrLen = arr.length,
bucketLen = maxValue + 1
// 存储
for (var i = 0; i < arrLen; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 0
}
bucket[arr[i]]++
}
// 将数据从bucket按顺序写入res中,控制仅仅输出前k个
let res = []
for (var j = 0; j < bucketLen; j++) {
while(bucket[j]-- > 0 && sortedIndex < k) {
res[sortedIndex++] = j
}
if(sortedIndex === k) {
break
}
}
return res
}复杂度分析:
|
//使用冒泡排序const countingSort = (arr, k) => { } |
|
借鉴快排的思想 function sort(arr, l, r, k) { function quicksort(arr, l, r) { |
|
/**
} // 原地建堆,从后往前,自上而下式建大顶堆(顶元素是堆中最大的。) } for(let i= k; i<arr.length; i++){ return heap; |
话不多说,来一道题目加深一下理解吧:
输入整数数组
arr,找出其中最小的k个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。示例 1:
示例 2:
限制:
0 <= k <= arr.length <= 100000 <= arr[i] <= 10000附赠leetcode地址:leetcode
The text was updated successfully, but these errors were encountered: