Samplitude

CLI generation and plotting of random variables:

$ samplitude "sin(0.31415) | sample(6) | round | cli"
0.0
0.309
0.588
0.809
0.951
1.0

The word samplitude is a portmanteau of sample and amplitude. This project also started as an étude, hence should be pronounced sampl-étude.

samplitude is a chain starting with a generator, followed by zero or more filters, followed by a consumer. Most generators are infinite (with the exception of range and lists and possibly stdin). Some of the filters can turn infinite generators into finite generators (like sample and gobble), and some filters can turn finite generators into infinite generators, such as choice.

Consumers are filters that necessarily flush the input; list, cli, json, unique, and the plotting tools, hist, scatter and line are examples of consumers. The list consumer is a Jinja2 built-in, and other Jinja2 consumers are sum, min, and max:

samplitude "sin(0.31415) | sample(5) | round | max | cli"
0.951

For simplicity, s8e is an alias for samplitude.

Generators

In addition to the standard range function, we support infinite generators

• exponential(lambd): lambd is 1.0 divided by the desired mean.
• uniform(a, b): Get a random number in the range [a, b) or [a, b] depending on rounding.
• gauss(mu, sigma): mu is the mean, and sigma is the standard deviation.
• normal(mu, sigma): as above
• lognormal(mu, sigma): as above
• triangular(low, high): Continuous distribution bounded by given lower and upper limits, and having a given mode value in-between.
• beta(alpha, beta): Conditions on the parameters are alpha > 0 and beta > 0. Returned values range between 0 and 1.
• gamma(alpha, beta): as above
• weibull(alpha, beta): alpha is the scale parameter and beta is the shape parameter.
• pareto(alpha): Pareto distribution. alpha is the shape parameter.
• vonmises(mu, kappa): mu is the mean angle, expressed in radians between 0 and 2*pi, and kappa is the concentration parameter, which must be greater than or equal to zero. If kappa is equal to zero, this distribution reduces to a uniform random angle over the range 0 to 2*pi.

Provided that you have installed the scipy.stats package, the

• pert(low, peak, high) distribution is supported.

We have a special infinite generator (filter) that works on finite generators:

• choice,

whose behaviour is explained below.

For input from files, either use words with a specified environment variable DICTIONARY, or pipe through

• stdin()

which reads from stdin.

If the file is a csv file, there is a csv generator that reads a csv file with Pandas and outputs the first column (if nothing else is specified). Specify the column with either an integer index or a column name:

>>> samplitude "csv('iris.csv', 'virginica') | counter | cli"
0 50
1 50
2 50

For other files, we have the file generator:

>>> s8e "file('iris.csv') | sample(1) | cli"
150,4,setosa,versicolor,virginica

Finally, we have combinations and permutations that are inherited from itertools and behave exactly like those.

>>> s8e "'ABC' | permutations | cli"

However, the output of this is rather non-UNIXy, with the abstractions leaking through:

>>> s8e "'HT' | permutations | cli"
('H', 'T')
('T', 'H')

So to get a better output, we can use an elementwise join elt_join:

>>> s8e "'HT' | permutations | elt_join | cli"
H T
T H

which also takes a seperator as argument:

>>> s8e "'HT' | permutations | elt_join(';') | cli"
H;T
T;H

This is already supported by Jinja's map function (notice the strings around join):

>>> s8e "'HT' | permutations | map('join', ';') | cli"
H;T
T;H

We can thus count the number of permutations of a set of size 10:

>>> s8e "range(10) | permutations | len"
3628800

The product generator takes two generators and computes a cross-product of these. In addition,

A warning about infinity

All generators are (potentially) infinite generators, and must be sampled with sample(n) before consuming!

Usage and installation

Install with

pip install samplitude

or to get bleeding release,

pip install git+https://github.com/pgdr/samplitude

Examples

This is pure Jinja2:

>>> samplitude "range(5) | list"
[0, 1, 2, 3, 4]

However, to get a more UNIXy output, we use cli instead of list:

>>> s8e "range(5) | cli"
0
1
2
3
4

To limit the output, we use sample(n):

>>> s8e "range(1000) | sample(5) | cli"
0
1
2
3
4

That isn't very helpful on the range generator, which is already finite, but is much more helpful on an infinite generator. The above example is probably better written as

>>> s8e "count() | sample(5) | cli"
0
1
2
3
4

However, much more interesting are the infinite random generators, such as the uniform generator:

>>> s8e "uniform(0, 5) | sample(5) | cli"
3.3900198868059235
1.2002767137709318
0.40999391897569126
1.9394585953696264
4.37327472704115

We can round the output in case we don't need as many digits (note that round is a generator as well and can be placed on either side of sample):

>>> s8e "uniform(0, 5) | round(2) | sample(5) | cli"
4.98
4.42
2.05
2.29
3.34

Selection and modifications

The sample behavior is equivalent to the head program, or from languages such as Haskell. The head alias is supported:

>>> samplitude "uniform(0, 5) | round(2) | head(5) | cli"
4.58
4.33
1.87
2.09
4.8

drop is also available:

>>> s8e "uniform(0, 5) | round(2) | drop(2) | head(3) | cli"
1.87
2.09
4.8

To shift and scale distributions, we can use the shift(s) and scale(s) filters. To get a Poisson distribution process starting at 15, we can run

>>> s8e "poisson(4) | shift(15) | sample(5) |cli"
18
21
19
22
17

or to get the Poisson point process (exponential distribution),

>>> s8e "exponential(4) | round | shift(15) | sample(5) |cli"
16.405
15.54
15.132
15.153
15.275

Both shift and scale work on generators, so to add sin(0.1) and sin(0.2), we can run

>>> s8e "sin(0.1) | shift(sin(0.2)) | sample(10) | cli"

Choices and other operations

Using choice with a finite generator gives an infinite generator that chooses from the provided generator:

>>> samplitude "range(0, 11, 2) | choice | sample(6) | cli"
8
0
8
10
4
6

Jinja2 supports more generic lists, e.g., lists of strings. Hence, we can write

>>> s8e "['win', 'draw', 'loss'] | choice | sample(6) | sort | cli"
draw
draw
loss
loss
loss
win

... and as in Python, strings are also iterable:

>>> s8e "'HT' | cli"
H
T

... so we can flip six coins with

>>> s8e "'HT' | choice | sample(6) | cli"
H
T
T
H
H
H

We can flip 100 coins and count the output with counter (which is collections.Counter)

>>> s8e "'HT' | choice | sample(100) | counter | cli"
H 47
T 53

The sort functionality works as expected on a Counter object (a dict type), so if we want the output sorted by key, we can run

>>> s8e "range(1,7) | choice | sample(100) | counter | sort | elt_join | cli" 42 # seed=42
1 17
2 21
3 12
4 21
5 13
6 16

There is a minor hack to sort by value, namely by swap-ing the Counter twice:

>>> s8e "range(1,7) | choice | sample(100) |
         counter | swap | sort | swap | elt_join | cli" 42 # seed=42
3 12
5 13
6 16
1 17
2 21
4 21

The swap filter does an element-wise reverse, with element-wise reverse defined on a dictionary as a list of (value, key) for each key-value pair in the dictionary.

So, to get the three most common anagram strings, we can run

>>> s8e "words() | map('sort') | counter | swap | sort(reverse=True) |
         swap | sample(3) | map('first') | elt_join('') | cli"
aeprs
acerst
opst

Using stdin() as a generator, we can pipe into samplitude. Beware that stdin() flushes the input, hence stdin (currently) does not work with infinite input streams.

>>> ls | samplitude "stdin() | choice | sample(1) | cli"
some_file

Then, if we ever wanted to shuffle ls we can run

>>> ls | samplitude "stdin() | shuffle | cli"
some_file

>>> cat FILE | samplitude "stdin() | cli"
# NOOP; cats FILE

The fun powder plot

For fun, if you have installed matplotlib, we support plotting, hist being the most useful.

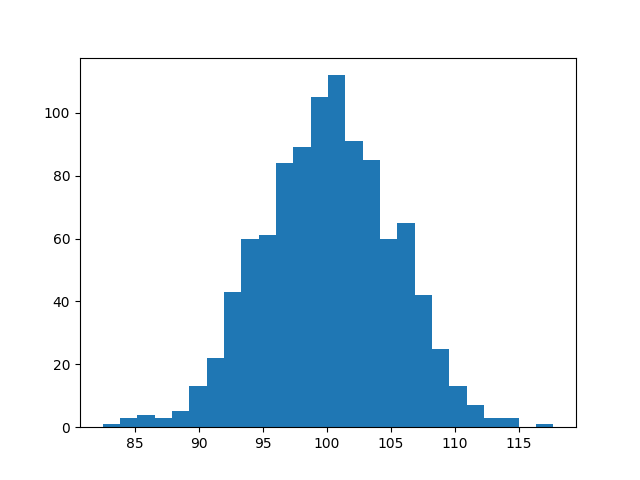
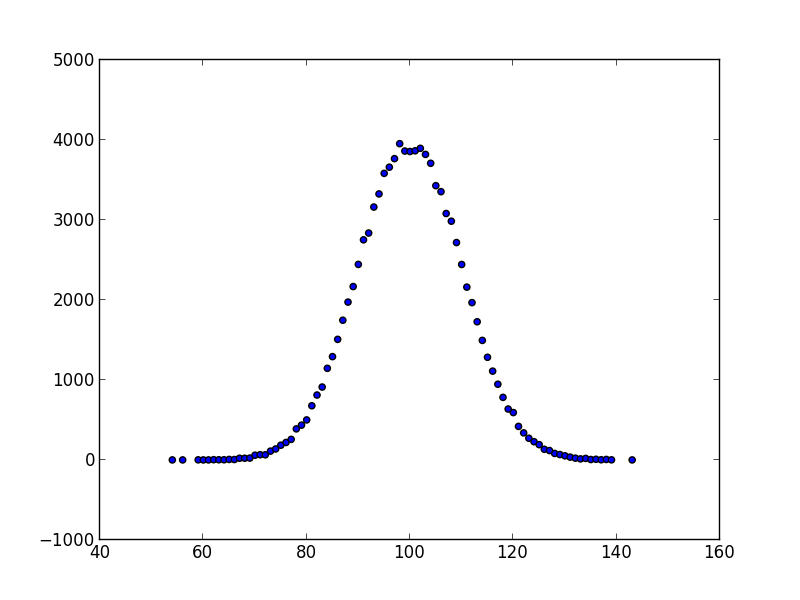
>>> samplitude "normal(100, 5) | sample(1000) | hist"

An exponential distribution can be plotted with exponential(lamba). Note that the cli output must be the last filter in the chain, as that is a command-line utility only:

>>> s8e "normal(100, 5) | sample(1000) | hist | cli"

To repress output after plotting, you can use the gobble filter to empty the pipe:

>>> s8e "normal(100, 5) | sample(1000) | hist | gobble"

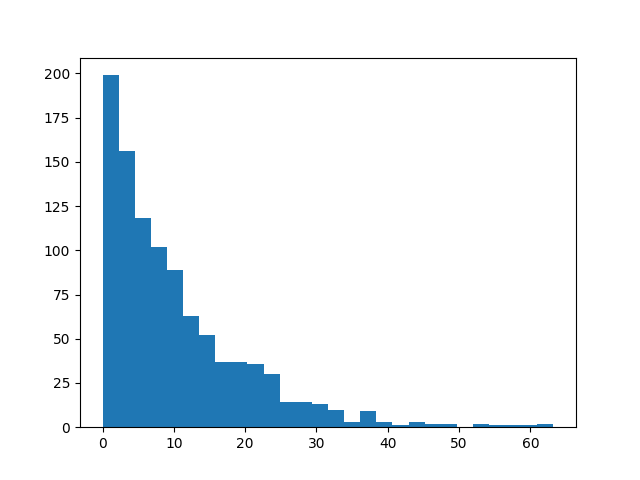
The pert distribution takes inputs low, peak, and high:

>>> s8e "pert(10, 50, 90) | sample(100000) | hist(100) | gobble"

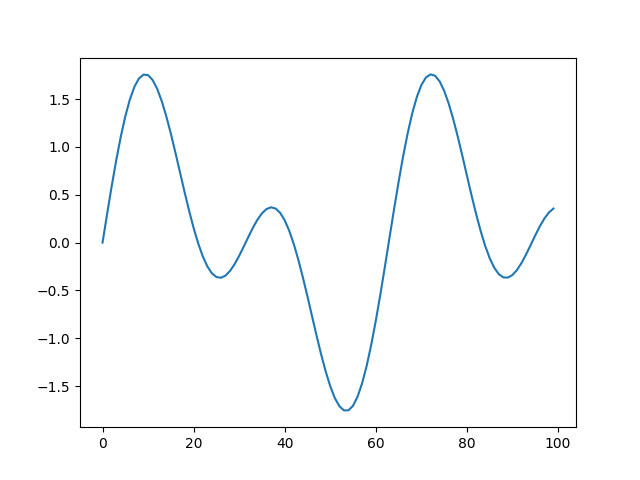
Although hist is the most useful, one could imaging running s8e on timeseries, where a line plot makes most sense:

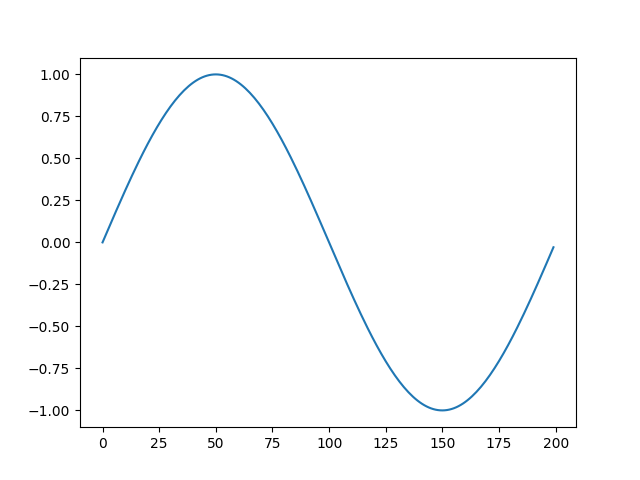
>>> s8e "sin(22/700) | sample(200) | line"

The scatter function can also be used, but requires that the input stream is a stream of pairs, which can be obtained either by the product generator, or via the pair or counter filter:

s8e "normal(100, 10) | sample(10**5) | round(0) | counter | scatter"

Fourier

A fourier transform is offered as a filter fft:

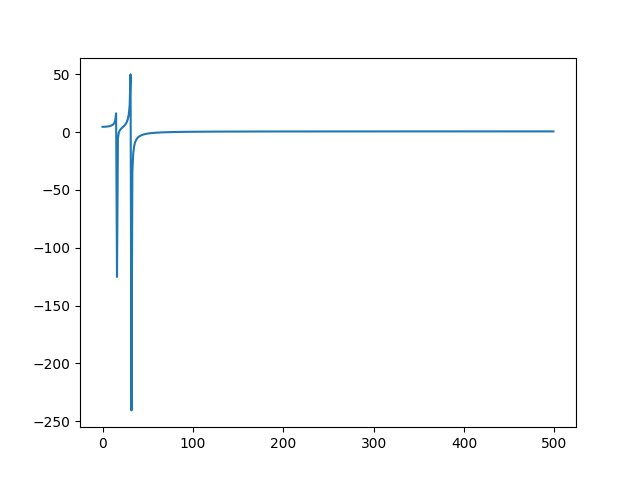
>>> samplitude "sin(0.1) | shift(sin(0.2)) | sample(1000) | fft | line | gobble"

Your own filter

If you use Samplitude programmatically, you can register your own filter by sending a dictionary

{'name1' : filter1,
 'name2' : filter2,
 #...,
 'namen' : filtern,
}

to the samplitude function.

Example: secretary problem

Suppose you want to emulate the secretary problem ...

Intermezzo: The problem

For those not familiar, you are a boss, Alice, who wants to hire a new secretary Bob. Suppose you want to hire the tallest Bob of all your candidates, but the candidates arrive in a stream, and you know only the number of candidates. For each candidate, you have to accept (hire) or reject the candidate. Once you have rejected a candidate, you cannot undo the decision.

The solution to this problem is to look at the first n/e (e~2.71828 being the Euler constant) candidates, and thereafter accept the first candidate taller than all of the n/e first candidates.

A Samplitude solution

Let normal(170, 10) be the candidate generator, and let n=100. We create a filter secretary that takes a stream and an integer (n) and picks according to the solution. In order to be able to assess the quality of the solution later, the filter must forward the entire list of candidates; hence we annotate the one we choose with (c, False) for a candidate we rejected, and (c, True) denotes the candidate we accepted.

def secretary(gen, n):
    import math
    explore = int(n / math.e)
    target = -float('inf')
    i = 0

    # explore the first n/e candidates
    for c in gen:
        target = max(c, target)
        yield (c, False)
        i += 1
        if i == explore:
            break

    _ok = lambda c, i, found: ((i == n-1 and not found)
                            or (c > target and not found))

    have_hired = False
    for c in gen:
        status = _ok(c, i, have_hired)
        have_hired = have_hired or status
        yield c, status
        i += 1
        if i == n:
            return

Now, to emulate the secretary problem with Samplitude:

from samplitude import samplitude as s8e

# insert above secretary function

n = 100
filters = {'secretary': secretary}

solution = s8e('normal(170, 10) | secretary(%d) | list' % n, filters=filters)
solution = eval(solution)  # Samplitude returns an eval-able string
cands = map(lambda x: x[0], solution)
opt = [s[0] for s in solution if s[1]][0]
# the next line prints in which position the candidate is
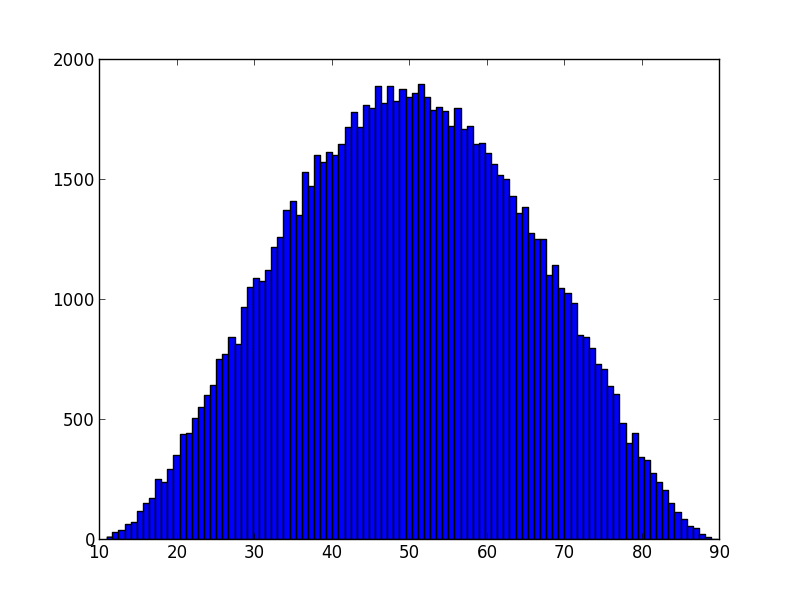
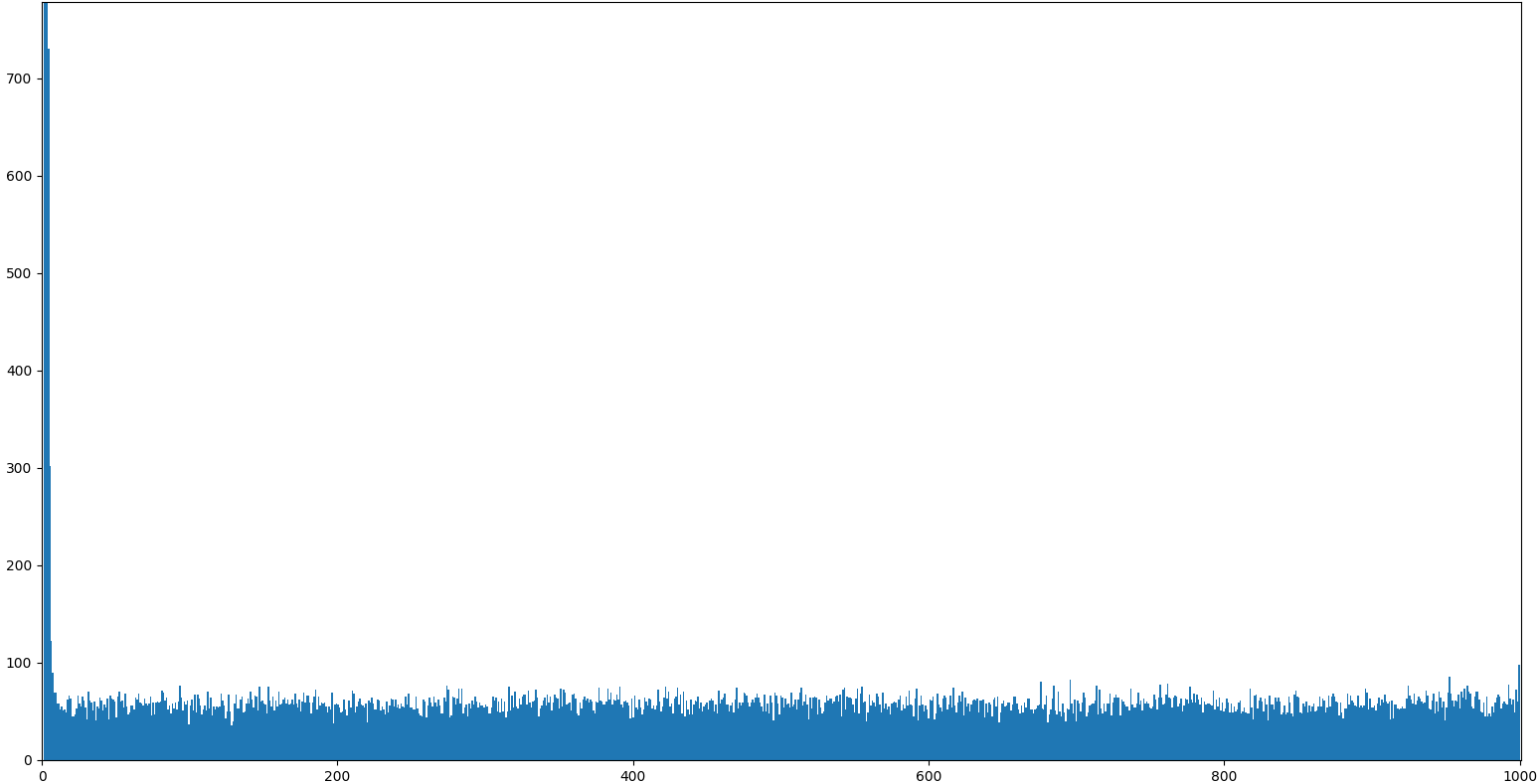
print(1+sorted(cands, reverse=True).index(opt), '/', n)

In about 67% of the cases we can expect to get one of the top candidates, whereas the remaining 33% of the cases will be uniformly distributed. Running 100k runs with a population of size 1000 reveals the structure.