110-BalancedBinaryTree

Balanced Binary Tree

Easy

Given a binary tree, determine if it is height-balanced.

Example 1:

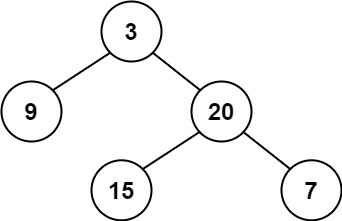
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

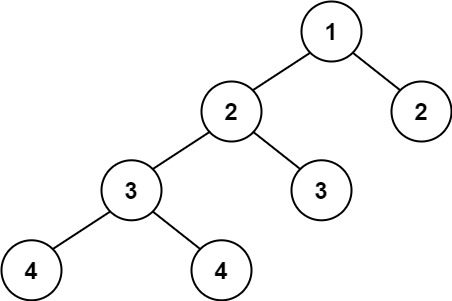
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• $-10^4$ <= Node.val <= $10^4$

Problem can be found in here!

Solution

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

Solution: Hash Table + Depth-First Search

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        if root is None:
            return True

        self.memo = {}
        subtrees_height_diff = abs(self.find_depth(root.left)-self.find_depth(root.right))
        is_tree_balanced = subtrees_height_diff < 2
        return is_tree_balanced and self.isBalanced(root.left) and self.isBalanced(root.right)

    def find_depth(self, node: Optional[TreeNode]) -> int:
        if node is None:
            return 0
        if node not in self.memo:
            self.memo[node] = max(self.find_depth(node.left), self.find_depth(node.right)) + 1

        return self.memo[node]

Explanation: The definition of a balanced binary tree is "a binary tree in which the left and right subtrees of every node differ in height by no more than 1." Therefore, we need to check whether the height difference between the left and right subtrees is no more than 1 for every tree node. To do so, we can simply iterate the whole binary tree through depth-first search (DFS). With a hash table, we can improve the time complexity to $O(n)$ instead of $O(n^2)$.

Time Complexity: $O(n)$, Space Complexity: $O(h)$ for the recursive stack, where h is the height of the binary tree. In worst case, h will be n for an unbalanced binary tree.