- solution: DGGS (https://vimeo.com/935616988/d9de7a97e9 min 49:00)
- UTM grid is not native to the sattelite
- advantage of DGGS: one global CRS and still no loss in resolution
- tiles of multiple local projections need to overlap. No comparision betwwen differnt zones -> DGGS is one global CRS
- DGGS Cells wrap arround faces -> seamingless
- vector world: sparse daat, few points from a couple of sites, tables with columns lon, lat and feature values, traditional databases postgis
- raster world: dense data, images
- Data Cube: https://esd.copernicus.org/articles/11/201/2020/
- ESA and ECMWF using zarr for ARD
- level 4 data: ARD
- data cubes allow fast loading of data, crucial for AI
- peta bytes of data
- like COG and STAC but more flexible chunking
- scaleable
- paralell reads and writs
Satellite images are traditionally stored and accessed in rectangular grids. Hereby, the surface of the earth is flattened to this 2D grid using a single global projection. This introduces distortions of shape and area, especially in more extreme latitudes. Discrete Global Grid Systems (DGGS) tessellate the surface of the earth with hierarchical cells of equal area, minimizing distortion and loading time of large geospatial datasets, which is crucial in spatial statistics and building Machine Learning models. Previous works focused on the creation of the grid themselves, as well as translating geographical coordinates to DGGS cell ids. Here we present a framework to store and access DGGS data.
- Current specification: OGC Topic 21 / ISO 19170
- Planned in future parts of the OGC specifications
- DGGS registry analog to EPSG.io
- DGGS data storage format
- 60 projections, one for each UTM zone
- 7 projections, one for each continent Equi7Grid (Bauer-Marschallinger et al., 2014)
- 20 projections: icosahedron
- cube with fixed orientation
- Hilbert curve like index
- hexagonal cells, fixed aperture of 7
- icosahedron with fixed orientation
- Gnomomic projection: Fast, distortions in both shape and area
- Hierarchical index
DGGRID (Sahr et al.)
- (Gibb 2016)
- FITS file format (Hivon et al. 2020)
- openEAGER
- has plug ins for elastic search and postGIS
- One can store the data in a traditional relational database, e.g. PostGIS or ClickHouse (column based)
- datase management system: Combines storage and analysis (e.g. SQL). We want to use all kinds of analysis languages instead
- Storing DGGS cell data in such a database produces an enourmous overhead in space
- report
- PostGIS vs ClickHouse
- PostGIS
- is an all prupose db -> Not optimized
- rowise (all properties of an element together). This is unsuitable for e.g. temperature mean, where we want to have all temperature values for all locations together in memory
- does not scale well (we need billions of rows)
- primarily single threaded
- Clickhouse
- column based db like n-dimensional array
- Good for immutable data (e.g. log files), terrible at mutation
- Multi threaded
- Uses pyramid
- Tile id analog to cell id in DGGS
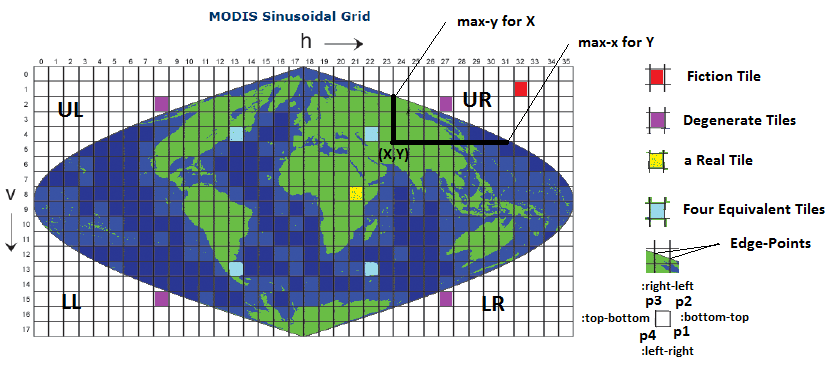
- Area and shape distortion depend on the projection. For instance, MODIS tiles use sinusoidal projection resulting in tiles having a equal area
- https://developers.planet.com/docs/planetschool/an-introduction-to-cloud-optimized-geotiffs-cogs-part-1-overview/
- ICOsahedral Nonhydrostatic model for wheather forfacsting
- developed by MPI for Meterology and DWD since 2001
- triangular grid on an icosahedron
- equal area, no issue of meridian convergence e.g. at the poles
- triangles have few neighbors: small discretization stencil, less communication, easier to parallalize in computing the diff. equations
- triangles are the most simplest polygon: Used to sescribe 3D meshes in vis, games, ...
- triangles are always flat in 3D: Easier to reason, faster compulations
- triangles have perfect sub-division and perfect nesting
- Think about a low res cloud terrain model and a high res soil model. Perfect nesting is required for integration to converve mass, energy and momentum
- hexagons have an undesirable geostrophic mode in modelling winds affected by coriolis force Niˇckovi´c et al. (2002)
- Wan et al. 2013
- Wheather models are a good example for DGGS (actual grid system where parent cells need to talk to child cells), Sattelite image ML is more a DGG (multi res is not that important unless multiple products of different resolutions are integrated)
- No projection e.g. Gnomonic or ISEA, just subdivide great circles. In a normal DGGS, the cell boundaries are re-projected to the sphere. ICON just re-rpjects the 20 base triangles of the icosahedron.
- ICON as a DGGS (Jubair et al. 2016)
- Grids for models from Germany (ICON), US (MPAS) and Japan (NICAM) are very similar (Jubair et al. 2016)
- ICON stores cell data in an unstructured way
- ICON data is dsigned for simulation, nnot for visualization
- climate modelling is limited by CPU/GPU and not IO (high performance and not high throughput), this data storage format might tot be the first priority
- Neighbors of a triangle vertex are the vertices of a hexagon centered around rthat triangle vertex. Hex traversal to get neighbors (Jubair et al. 2016)](https://diglib.eg.org/xmlui/bitstream/handle/10.2312/vmv20161355/161-168.pdf?sequence=1)
- rotate the pentagon outside the himalaya (high velocoty due to orograpphy -> eror in numerical simulations)
-
alll shapes can be created from the same base grid (composing triangles into hexagons)
-
triangle
- only aperture 4
- most simple
- perfect nesting
-
diamond
- only aperture 4
- oerfect nesting
-
hexagon
- apertures 3,4 and 7
- inconsistent coriolis force (See ICON)
- Most common packages, OGC definition): 1D string
- Issue: Need to squeeze 2D surface to 1D index using space filling curves
- These curves are streets restrictimg our movements! (Convolutions, BBox queries etc.)
- Hilbert curve: Google S2
- Peano curve: Geohash
- https://dl.acm.org/doi/pdf/10.1145/93605.98742
- https://www.youtube.com/watch?v=z3PaGIQTFSE
- Coordinate transformations introduces error in physical floating point geo coordinates , especially a problem at global scale https://discourse.pangeo.io/t/example-which-highlights-the-limitations-of-netcdf-style-coordinates-for-large-geospatial-rasters/4140. DGGS is discrete: no floating point errors
Ways of inexing DGGS data:
-
1D indices
- space filling curves
- Google S2: Similar to Hilbert curves
- prefix codes
- fast: get parents and distance (how many bits are shared)
- slow: BBox (need polyfill, still better than point in any polygon queries)
- examples
- Uber H3: 3 bits per resolution
- Generalized place index based on generalized balanced ternary, (Sahr)
- Microsoft Bing Quadkeys
- this is an embedding to reduce 2D space in just one dimension while preserving good neighborship. This is helpful in Deep Learning (Similar to embedding)
- good for points: The binary search tree is a fractal as well
- space filling curves
-
2D indies
- geographical grids using lon/lat
- (x, y) in a plane of a foldable figure of the polyhedron (e.g. DGGRID projtri)
- Good for polygons: Just need to check the boundaries, i.e. 2 intervals with 4 points for a bounding box. Every index between the interval borders are contained as well.
-
3D indices
- no projection at all :)
-
1D index of HEALPIX can be ordered in two different ways
- RING: Good for global patterns, Fourier Transformation
- Nested: Good for local patterns, Wavelet Transformation, Neighbor search
-
2D index for hexagonal convolutions
- HexagDLy uses offset coordinates
- Uber uses axial coordinates
- HEXACONV gives theoretical background about this
- group convolution instead of just translational convolution: Rotational equivariance
- higher degree of symmetry: Less parameters needed to train the network
- uses offset coords for most efficient data storage [Foo et al.](https://www.sciencedirect.com/science/article/pii/S2352711018302723#b12
- downside of axial coordinates: Space inefficient due to paralellogram. We don't care here because we store global data and zarr allows empty chunks
- should be 2D to be optimized for ANN kernels (Bounding box queries) and chunking (allowing tiling), index interval is always a continous interval in geo space as well
- PROJTRI: (face, x, y) triangles that need further processing to be stored in a matrix
- Q2DI: (quad, i, j)
- hexagons alter between pointy top (Class I, i axis horizontal) and flat top (Class II, j axis vertical)
- integers are lossless to compute
- files from DGGRID are small
- But some points have are on a 3rd face
- Already a rectangle (Rhombus shear done by DGGRID)
- Q2DD: (quad, x, y) floats are big and lossy, only 2 faces per map, rhombus
- Natural coordinate dimensions are both space and time
- Both can be aggregated and can be stored in different resolutions
- Important use case: Simulation outputs where all time and space points are available
- Save a separate dataset for each combination of time and space resolution in GEMS DKRZ healpix data
- DGGS shttps://docs.ogc.org/as/20-040r3/20-040r3.html
- based on zarr: Cloud optimized, multi dimenional, flexible chunking
- data is stored in a list of maps
- each map is a rectangular data cube
- each map may contain multiple neighboring polyhedron faces (e.g. 2 triangles of an icosahedron)
- each map has a matrix as locations. This allows more local chunking i.e. tiling. One could also make an array of arrays with incremental lengths for a triangular face on an icosahedron, but this would only allow stripes but not tiles.
- The polyhedron to be used (One of the 5 platonic solids)
- The orientation of the polyhedron relative to the sphere
- The radius of the sphere (e.g. authalic earth)
- list of faces
- mappings from faces to maps
- grid for each map: origin vector, unit vectors (grid lengths), n grid points for each direction, list of undef points
- Programm to be used for grid construction (e.g. DGGRID v 7.8)
- Other meta data as Climate and Forecast (CF) attributes
- Up to now: The grid defines only the 2D surface of the earth.
- Need altitude e.g. to represent ocean tides
- Now: Equal volume of cells
- Depth: Put a vector of values at cell center: https://www.mdpi.com/2220-9964/9/4/233
- https://www.mdpi.com/2220-9964/9/4/233
- Want to describe movement from one cell to a neighbor.
- Need to index not cells but edges between two cells
- Useful to describe streams of water, wind and molecules
- Uber H3 can be extended to address edges (not implemented yet)
- Any works on representing speed and force relative to cells?
- We have a vector (x,y,z) on cartesian coordinates for every point in cartesean 3D space. Do we need to reproject the vector to axes of the DGGS? Which axis in a hexagonal grid if data i stored in offset coords?
- What agout providing cached aggragations not only ove space (resolution) but also time?
- Data should be shaped in tensors with 2 spatial dimensions
- To save it in a n dimensional array
- To use it in CNN
- To view it using bbox queries
- quasi hexagonal kernel combining multiple rectangular kernels
- Hexaconv just one rectangular kernel, axial coords, some edges have weight 0
-
A unstaggered: Just store the variable at the center of a cell
-
B t to E: store also variables at corner or mid points of edges
-
C: e.g. store wind speed at center and masses at vertices, becomes more and more popular
-
vertical staggering: e.g. no flux at top or bottom
-
Can we just overlay ISEA4H, ISEA4D and ISEA4T to archive staggering?