P4994.cpp

#include <cstdio>

using namespace std;

int main()
{
    int M;
    scanf("%d", &M);
    int itemN = 1;   // 第n项
    int itemNP1 = 1; // 第n+1项
    int n = 1;       // 当前的n
    while (true)
    {
        int modN = itemN % M;         // f(n) mod 2
        int modNP1 = itemNP1 % M;     // f(n+1) mod 2
        if (modN == 0 && modNP1 == 1) // 找到满足要求的n了
            break;
        itemN = itemNP1;         // 第n+1项
        itemNP1 = modN + modNP1; // 第n+2项（取模后再运算不会影响结果）
        n++;
    }
    printf("%d", n);
    return 0;
}

/*
    这题需要从递推出的斐波那契数列中找出匹配项。

    观察可以发现，自始至终运算其实只涉及到了第n项和第n+1项，实际上我只需要利用两个变量进行递推即可，没有必要开一个数组。

    程序中还会用到模运算的性质：(a+b) mod p = (a mod p + b mod p) mod p

    借此我可以让两个变量的值一直保持在[0,M)的范围内，使得程序中用整型int数据类型就能进行表示和运算。

    * 注：题目输出限定n是>0的正整数。

        - SomeBottle 2023.3.6
*/

/*
# 终于结束的起点

## 题目背景

> 终于结束的起点
> 终于写下句点
> 终于我们告别
> 终于我们又回到原点
> ……

一个个 OIer 的竞赛生涯总是从一场 NOIp 开始，大多也在一场 NOIp 中结束，好似一次次轮回在不断上演。
如果这次 NOIp 是你的起点，那么祝你的 OI 生涯如同夏花般绚烂。
如果这次 NOIp 是你的终点，那么祝你的 OI 回忆宛若繁星般璀璨。
也许这是你最后一次在洛谷上打比赛，也许不是。
不过，无论如何，祝你在一周后的比赛里，好运。

当然，这道题也和轮回有关系。

## 题目描述

广为人知的斐波拉契数列 $\mathrm{fib}(n)$ 是这么计算的

![](https://cdn.luogu.com.cn/upload/pic/41010.png )

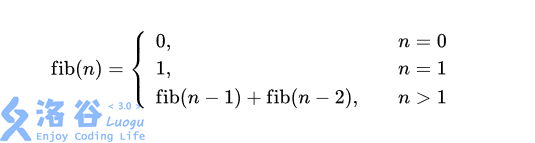
也就是 $0, 1, 1, 2, 3, 5, 8, 13 \cdots$，每一项都是前两项之和。

小 F 发现，如果把斐波拉契数列的每一项对任意大于 $1$ 的正整数 $M$ 取模的时候，数列都会产生循环。

当然，小 F 很快就明白了，因为 ($\mathrm{fib}(n - 1) \bmod M$) 和 ($\mathrm{fib}(n - 2) \bmod M)$ 最多只有 $M ^ 2$ 种取值，所以在 $M  ^ 2$ 次计算后一定出现过循环。


甚至更一般地，我们可以证明，无论取什么模数 $M$，最终模 $M$ 下的斐波拉契数列都会是 $0, 1, \cdots, 0, 1, \cdots$。

现在，给你一个模数 $M$，请你求出最小的 $n > 0$，使得 $\mathrm{fib}(n) \bmod M = 0, \mathrm{fib}(n + 1) \bmod M = 1$。

## 输入格式

输入一行一个正整数 $M$。

## 输出格式

输出一行一个正整数 $n$。

## 样例 #1

### 样例输入 #1

```
2
```

### 样例输出 #1

```
3
```

## 样例 #2

### 样例输入 #2

```
6
```

### 样例输出 #2

```
24
```

## 提示

#### 样例 1 解释

斐波拉契数列为 $0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \cdots$，在对 $2$ 取模后结果为 $0, 1, 1, 0, 1, 1, 0, 1, 1, 0, \cdots$。

我们可以发现，当 $n = 3$ 时，$f(n) \bmod 2= 0, f(n + 1) \bmod 2 = 1$，也就是我们要求的 $n$ 的最小值。

#### 数据范围

对于 $30\%$ 的数据，$M \leq 18$；

对于 $70\%$ 的数据，$M \leq 2018$；

对于 $100\%$ 的数据，$2 \leq M \leq 706150=$`0xAC666`。

#### 提示

如果你还不知道什么是取模 $(\bmod)$，那我也很乐意告诉你，模运算是求整数除法得到的余数，也就是竖式除法最终「除不尽」的部分，也即
$$a \bmod M =k \iff a = bM + k\ (M > 0, 0 \leq k < M)$$
其中 $a, b, k$ 都是非负整数。

如果你使用 `C` / `C++`，你可以使用 `%` 来进行模运算。

如果你使用 `Pascal`，你可以使用 `mod` 来进行模运算。
*/