Skip to content

Latest commit

 

History

History
442 lines (393 loc) · 17.3 KB

README.md

File metadata and controls

442 lines (393 loc) · 17.3 KB

动态规划：买卖股票的最佳时机系列问题

这是一套经典的动态规划题目，题目主干都是给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格，在不同的情况下求在什么时候买卖以获取最大利润。

  • 121题是只能买卖一次的情况下求最大利润；
  • 122题可以买卖任意多次；
  • 188题是前面三题的泛化版本，给定参数k，求买卖k次情况下的最大利润；
  • 309题是在122题买卖任意多次的基础上加上冷冻期即T+1才能卖出。

其中买卖k次的188题是标准的三维动态规划题，用解这题的通用方可以稍加改造就能解决前三题，当然前三题也有单独的特定简单解法，这里为了练习还是重点看动态规划的解决方法。

在188题的基础上可以再变形出更多题目，比如现在这些题都是最多只能持有1股，如果可以持有n股（每天只能买入或卖出1股），也能用这个188题的三维DP通解来解决。

121. 买卖股票的最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例1：

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
    注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例2：

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解：

第一种方法：由于一次交易操作，可以通过记录最小价格，计算最大利润的方式，空间换时间，时间复杂度O(n)

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n<=1) return 0;
        int res = 0;
        int min_price = prices[0];
        for (int i=0;i<n;i++)
        {
            res = max(res, prices[i] - min_price);
            min_price = min(min_price, prices[i]);
        }
        return res;
    }
};

第二种方法：DP动态规划，与下面122题相比，由于只能一次交易操作，第i天的状态就不止“买入”和“卖出”两种状态，而是“不操作”、“买入”、“卖出”三种状态。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n<=1) return 0;
        vector<vector<int>> dp (n, vector<int> (2,0));
        
        // 状态 dp[i][j] 表示：在索引为 i 的这一天，用户手上状态为 j 所获得的最大利润。

        // 0：用户手上不持股所能获得的最大利润，特指卖出股票以后的不持股，非指没有进行过任何交易的不持股
        // 1：用户手上持股所能获得的最大利润

        // 注意：因为题目限制只能交易一次，因此状态只可能从 1 到 0，不可能从 0 到 1

        dp[0][0] = 0;  
        dp[0][1] = -prices[0]; 

        // 状态转移方程：
        // dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]) 今天不持有股票，可以昨天不持有rest下来，也可以是昨天持有，今天卖了股票
        // dp[i][1] = max(dp[i - 1][1], - prices[i]) 今天因为持有股票，可以是昨天就持有，今天刚买的，因为只进行交易一次，所以只会减一个
        
        for (int i=1;i<n;i++)
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = max(dp[i - 1][1], - prices[i]); 
        }
        return dp[n-1][0];
    }
};

122. 买卖股票的最佳时机 II

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1：

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

解：

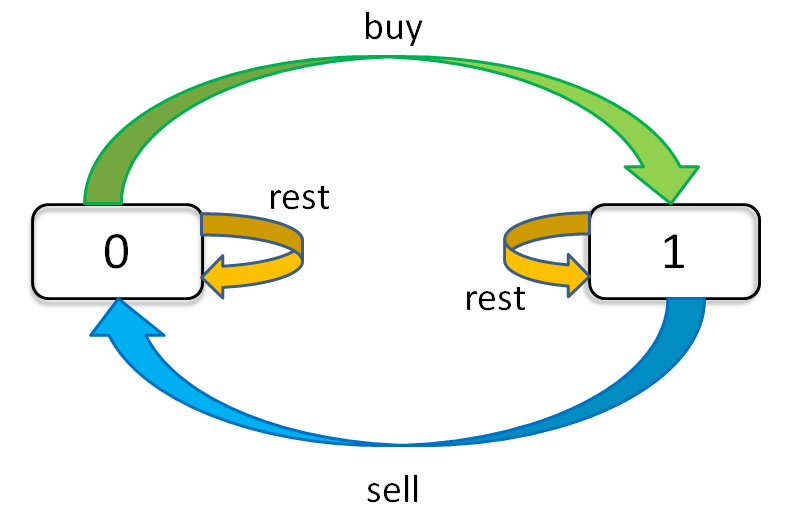
###标准二维DP动态规划，第i天只有两种状态，不持有或持有股票，当天不持有股票的状态可能来自昨天卖出或者昨天也不持有，同理，当天持有股票的状态可能来自昨天买入或者昨天也持有中，取最后一天的不持有股票状态就是问题的解。（没有交易次数限制）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n<=1) return 0;
        vector<vector<int>> dp (n, vector<int> (2,0));
        dp[0][0] = 0; // 不持有股票，持有现金
        dp[0][1] = -prices[0]; // 持有股票
        for (int i=1;i<n;i++)
        {
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }
        return dp[n-1][0];
    }
};

第三种方法：注意一下状态转移方程，新状态只和相邻的一个状态有关，其实不用整个 dp 数组，只需要一个变量储存相邻的那个状态就足够了，这样可以把空间复杂度降到 O(1）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n<=1) return 0;
        int dp_i_0= 0; 
        int dp_i_1 = -prices[0]; 
        for (int i=1;i<n;i++)
        {
            dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
            dp_i_1 = max(dp_i_1, dp_i_0 - prices[i]);
        }
        return dp_i_0;
    }
};

123. 买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1：

输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例2：

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。   
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。   
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例3：

输入: [7,6,4,3,1] 
输出: 0 
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。

解：

标准的三维DP动态规划，三个维度，第一维表示天，第二维表示交易了几次，第三维表示是否持有股票。与下面188题买卖股票4一样的代码，把交易k次定义为2次。当然也可以把内层的for循环拆出来，分别列出交易0次、1次、2次的状态转移方程即可

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n =prices.size();
        if (n<=1) return 0;
        int k = 2;
        vector<vector<vector<int>>> dp (n, vector<vector<int>> (k+1, vector<int>(2, 0)));
        // 初始状态
        for (int j =0; j<k+1;j++)
        {
            dp[0][j][0] = 0; // sell 不持有股票
            dp[0][j][1] = -prices[0]; // buy 持有股票
        }
        for (int i=1;i<n;i++)
        {
            for (int j=k;j>=1;j--)  
            // 从大到小进行遍历，因为计算当前K的值，只依赖K-1和i-1情况下的值，
            // 从大到小可以省去一个维度的数组，更新上一次计算的结果即可
            {
                dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1]+ prices[i]);
                dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i]);
            }
        }
        return dp[n-1][k][0];
    }
};

188. 买卖股票的最佳时机 IV

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k笔 交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1：

输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例2：

输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
     随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

解：

1. 标准的三维DP动态规划，三个维度，第一维表示天，第二维表示交易了几次，第三维表示是否持有股票。但是注意内存超限的问题，最大交易次数大于n/2时，等价于交易次数无限制

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        if (n<=1) return 0;
        if  (k>n/2) // 相当于没有交易次数限制
        {
            int res = 0;
            for (int i=1;i<n;i++)
            {
                if (prices[i] > prices[i-1])
                {
                    res += prices[i] - prices[i-1];
                }
            }
            return res;
        }
        vector<vector<vector<int>>> dp (n, vector<vector<int>> (k+1, vector<int>(2,0)));
        for (int j=0;j<k+1;j++)
        {
            dp[0][j][0] = 0;
            dp[0][j][1] = -prices[0];
        }
        for (int i=1;i<n;i++)
        {
            for(int j=k;j>=1;j--)
            {
                dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i]);
                dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i]);  // buy的时候算交易一次，
            }
        }
        return dp[n-1][k][0];
    }
};

2. 标准的三维DP动态规划，三个维度，第一维表示天，第二维表示交易了几次，第三维表示是否持有股票。

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        if (n<=1) return 0;
        if (k>n/2)
        {
              int dp_i_0= 0; 
              int dp_i_1 = -prices[0]; 
              for (int i=1;i<n;i++)
              {
                  dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
                  dp_i_1 = max(dp_i_1, dp_i_0 - prices[i]);
              }
              return dp_i_0;
        }
        vector<vector<vector<int>>> dp(n, vector<vector<int>> (k+1, vector<int>(2,0)));
        for (int j=0;j<k+1;j++)
        {
            dp[0][j][0] = 0;
            dp[0][j][1] = -prices[0];
        }
        for (int i=1;i<n;i++)
        {
            for (int j=k;j>=1;j--)
            {
                dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i]);
                dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i]);
            }
        }
        return dp[n-1][k][0];
    }
};

309. 最佳买卖股票时机含冷冻期

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

  • 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
  • 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

示例：

输入: [1,2,3,0,2]
输出: 3 
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

解：

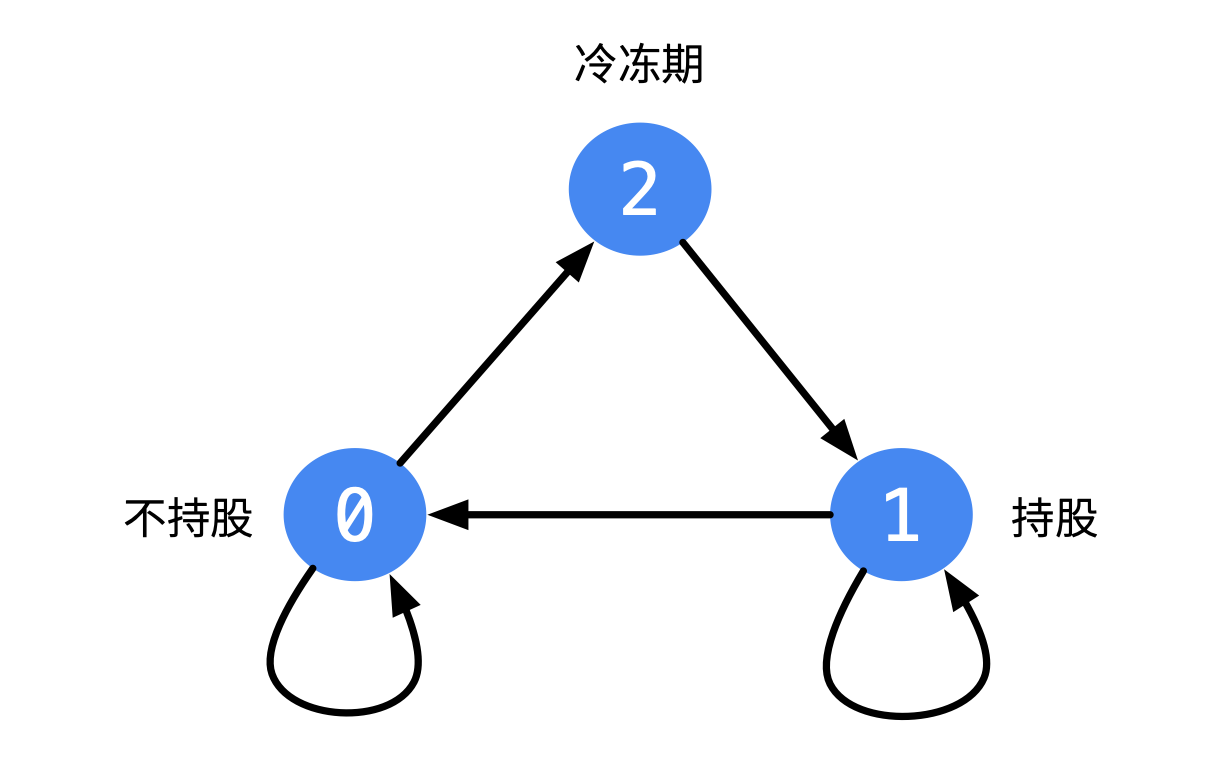
  • 不持股可以由这两个状态转换而来：（1）昨天不持股，今天什么都不操作，仍然不持股。（2）昨天持股，今天卖了一股。
  • 持股可以由这两个状态转换而来：（1）昨天持股，今天什么都不操作，仍然持股；（2）昨天处在冷冻期，今天买了一股；
  • 处在冷冻期只可以由不持股转换而来，因为题目中说，刚刚把股票卖了，需要冷冻 1 天。

1. DP动态规划，两个维度，第一维表示天，第二维表示状态。0：不持有股票，1：持有股票，2：处于冷冻期

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if(n<=1) return 0;
        vector<vector<int>> dp (n, vector<int>(3,0));
        dp[0][0] = 0; // 不持有股票
        dp[0][1] = -prices[0]; // 持有股票
        dp[0][2] = 0; // 处于冷冻期
        for (int i=1;i<n;i++)
        {
            //第i天不持有股票的情况有两种
            //a.第i-1天也不持有股票
            //b.第i-1天持股给卖了
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
            //第i天持有股票有两种情况
            //a.第i-1天也持有股票，第i天不操作，
            //b.第i-1天处于冷冻期，在第i天买入
            dp[i][1] = max(dp[i-1][1], dp[i-1][2]-prices[i]);
            //第i天是冷冻期只有一种情况:处在冷冻期只可以由不持股转换而来
            dp[i][2] = dp[i-1][0];
        }
        //最后最大利润为最后一天，不持有股票或者进入冷冻期的情况
        return max(dp[n-1][0], dp[n-1][2]);
    }
};

2. 优化，减少空间复杂度

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if(n<=1) return 0;
        int dp_i_0 = 0;
        int dp_i_1 = -prices[0];
        int dp_i_2 = 0;
        for (int i=1;i<n;i++)
        {
            int temp =dp_i_0;
            dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
            dp_i_1 = max(dp_i_1, dp_i_2 - prices[i]);
            dp_i_2 = temp;
        }
        return max(dp_i_0,dp_i_2);
    }
};

714. 买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每次交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

示例：

输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:  
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

解：

1. DP动态规划，两个维度，第一维表示天，第二维表示状态。0：不持有股票，1：持有股票

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        if (n<=1) return 0;
        vector<vector<int>> dp(n,vector<int>(2,0));
        dp[0][0] = 0;
        dp[0][1] = -prices[0]-fee;
        for (int i=1;i<n;i++)
        {
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee);
        }
        return dp[n-1][0];
    }
};

2. 优化，减少空间复杂度

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        if (n<=1) return 0;
        int dp_i_0 = 0;
        int dp_i_1 = -prices[0]-fee;
        for (int i=1;i<n;i++)
        {
            dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
            dp_i_1 = max(dp_i_1, dp_i_0 - prices[i] -fee);
        }
        return dp_i_0;
    }
};

参考