sort.md

排序

常考排序

快速排序

void QuickSort(vector<int>& nums, int n){
    // 思路：把一个数组分为左右两段，左段小于右段
    quickSort(nums, 0, n - 1);
}

// 原地交换，所以传入交换索引
void quickSort(vector<int>& nums, int start, int end) {
    if (start < end) {
        // 分治法：divide
        int pivot = partition(nums, start, end);
        quickSort(nums, 0, pivot-1);
        quickSort(nums, pivot+1, end);
    }
}
// 分区
int partition(vector<int>& nums, int start, int end){
    // 选取最后一个元素作为基准pivot
    int p = nums[end];
    int i = start;
    // 最后一个值就是基准所以不用比较
    for (int j = start; j < end; j++) {
        if (nums[j] < p) {
            swap(nums[i], nums[j]);
            i++;
        }
    }
    // 把基准值换到中间
    swap(nums[i], nums[end]);
    return i;
}

归并排序

void MergeSort(vector<int>& nums){
    if(nums.size() <= 1) return;
    mergeSort(nums, 0, nums.size() - 1);
}

void mergeSort(vector<int>& nums, int start, int end){
    if (start < end) {
        // 分治法：divide 分为两段
        int mid = (start + end) / 2;
        mergeSort(nums, start, mid);
        mergeSort(nums, mid + 1, end);
        // 合并两段数据
        merge(nums, start, mid, end);
    }
}

void merge(vector<int>& nums, int start, int mid, int end){
    vector<int> temp(end - start + 1, 0);
    int i = start;
    int j = mid + 1;
    int k = 0;

    while (i <= mid && j <= end) {
        temp[k++] = (nums[i] <= nums[j]) ? nums[i++] : nums[j++]; // 谁小合并谁
    }

    // 剩余部分合并
    while (i <= mid) {
        temp[k++] = nums[i++];
    }

    while (j <= end) {
        temp[k++] = nums[j++];
    }

    for (i = 0; i < k; i++) {
        nums[start + i] = temp[i];
    }
}

堆排序

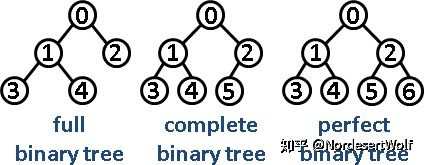
用数组表示的完美二叉树 complete binary tree

完美二叉树 VS 其他二叉树

动画展示

核心代码

//堆排序
void heapSort(vector<int>& nums){
    // 1、无序数组nums
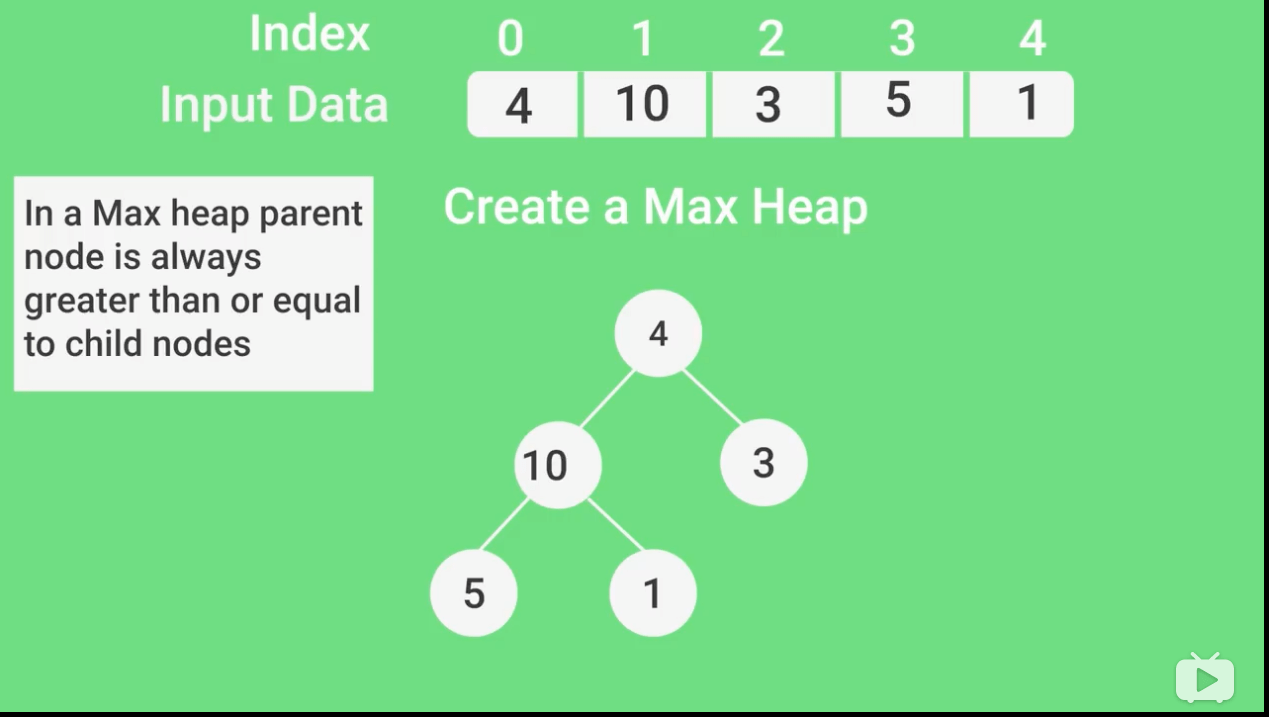
    // 2、将无序数组nums构建为一个大根堆
    buildMaxHeap(nums);

    // 3、交换nums[0]和nums[nums.size()-1]
    // 4、然后把前面这段数组继续下沉保持堆结构，如此循环即可
    int len = nums.size();  //此处len需要变换,单独拎出来
    for (int i = nums.size() - 1; i > 0; i--) {
        swap(nums[0], nums[i]);  // 从后往前填充值
        len--;                   // 前面的长度也减一
        heapHelper(nums, 0, len);
    }
}

// 建立大顶堆
void buildMaxHeap(vector<int>& nums){
    int length = nums.size();
    for (int i = length / 2; i >= 0; i--) {
        heapHelper(nums, i, length);
    }
}

//堆调整
void heapHelper(vector<int>& nums, int i, int length){
    int left = 2 * i + 1;  // 左节点索引(从0开始，所以左节点为i*2+1)
    int right = 2 * i + 2; // 右节点索引
    int largest = i;

    // largest保存根、左、右三者之间较大值的索引
    // 存在左节点，左节点值较大，则取左节点
    if (left < length && nums[left] > nums[largest]) {
        largest = left;
    }
    // 存在有节点，且值较大，取右节点
    if (right < length && nums[right] > nums[largest]) {
        largest = right;
    }

    // 如果非根节点较大，则继续递归
    if (largest != i) {
        swap(nums[i], nums[largest]);
        heapHelper(nums, largest, length);
    }
}

参考

十大经典排序

二叉堆

练习

• 手写快排、归并、堆排序