Sequential Information Processing
Remember! Please Download the Penn TreeBank (PTB) dataset manually first! And copy it into ./dataset directory. Never mind. I have done it.
RNN尤其是LSTM的提出是具有创造性价值的,相比于NN的函数拟合能力,CNN的视觉特征提取能力,RNN更着眼于理解和记忆。如果说CNN是视觉神经,那么RNN就是脑前庭上皮组织。
RNN的前向传播:
RNN的反向传播:
注:以上两图中的C应为Loss L
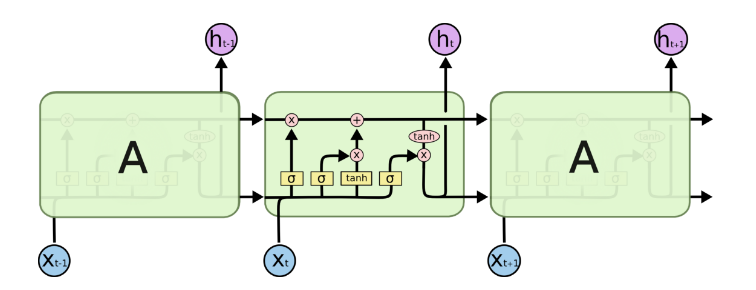
LSTM解决了Vanilla RNN对于长文本梯度消失的问题。二者区别详见 RNN与LSTM的区别
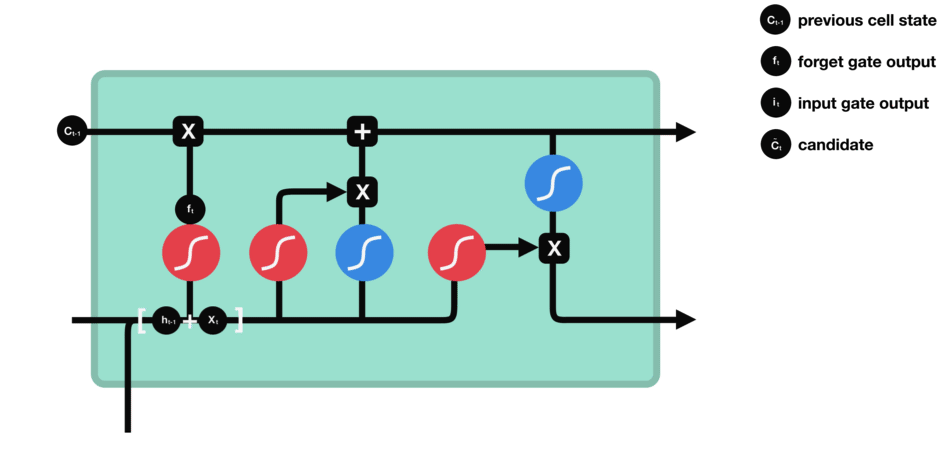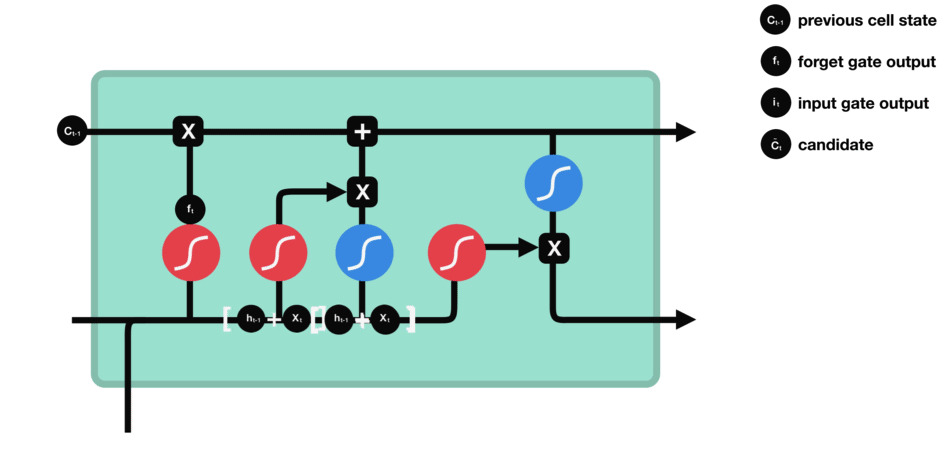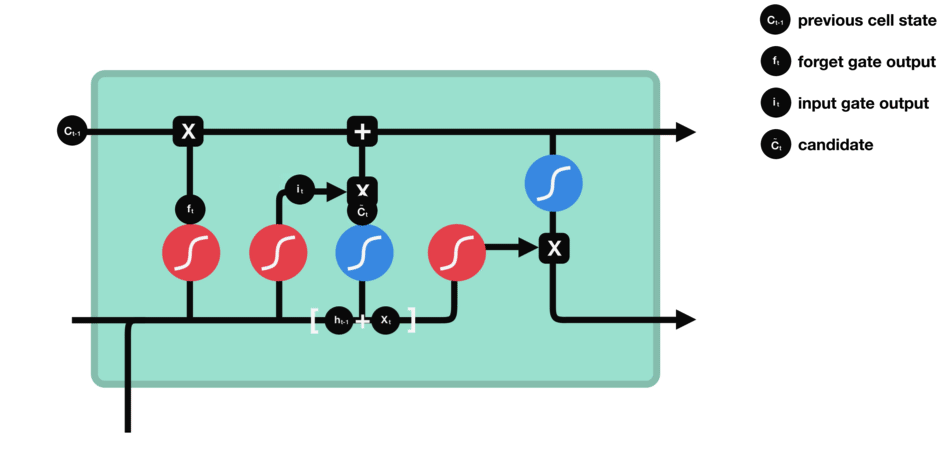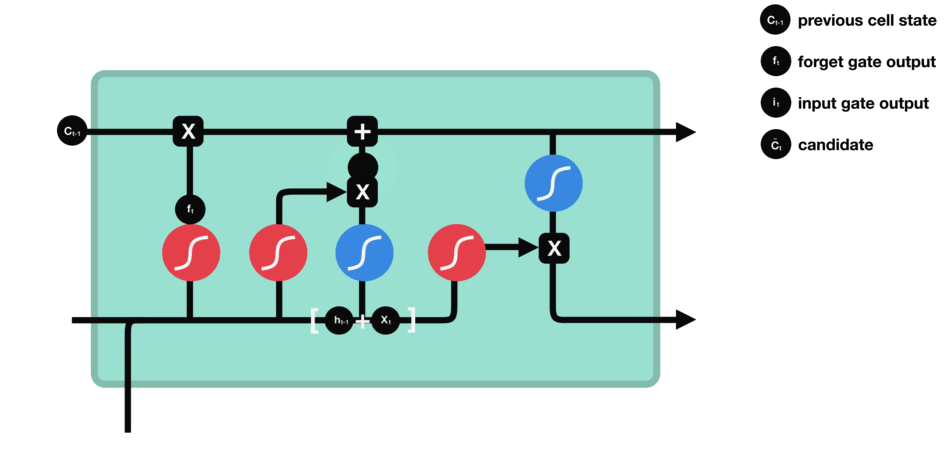
具体的公式就这些: $$\begin{array}{l} i=\sigma\left(W_{i i} x+b_{i i}+W_{h i} h+b_{h i}\right) \ f=\sigma\left(W_{i f} x+b_{i f}+W_{h f} h+b_{h f}\right) \ g=\tanh \left(W_{i g} x+b_{i g}+W_{h g} h+b_{h g}\right) \ o=\sigma\left(W_{i o} x+b_{i o}+W_{h o} h+b_{h o}\right) \ c^{\prime}=f * c+i * g \ h^{\prime}=o * \tanh \left(c^{\prime}\right) \end{array}$$ 简单来说就是,LSTM一共有三个门,输入门,遗忘门,输出门。
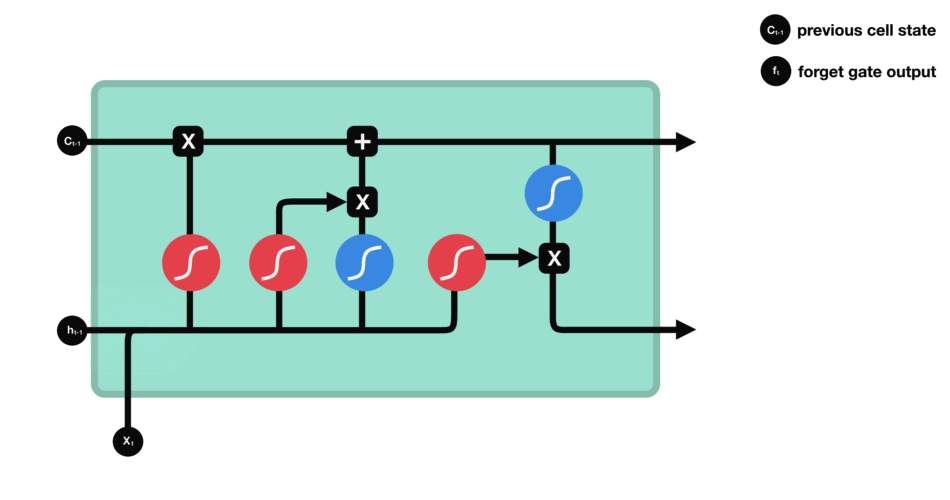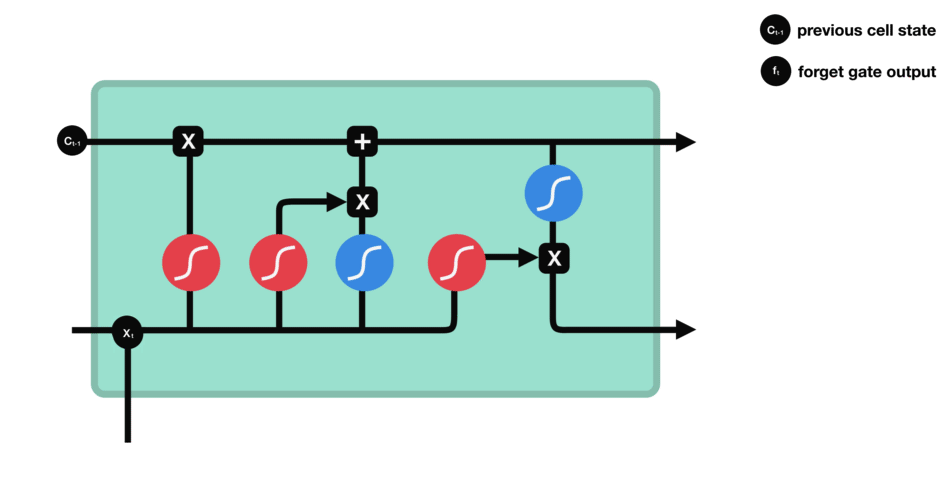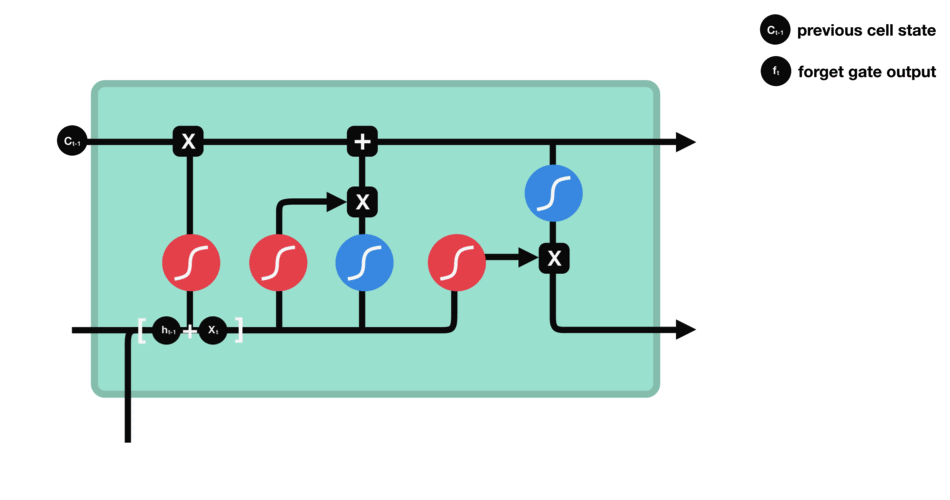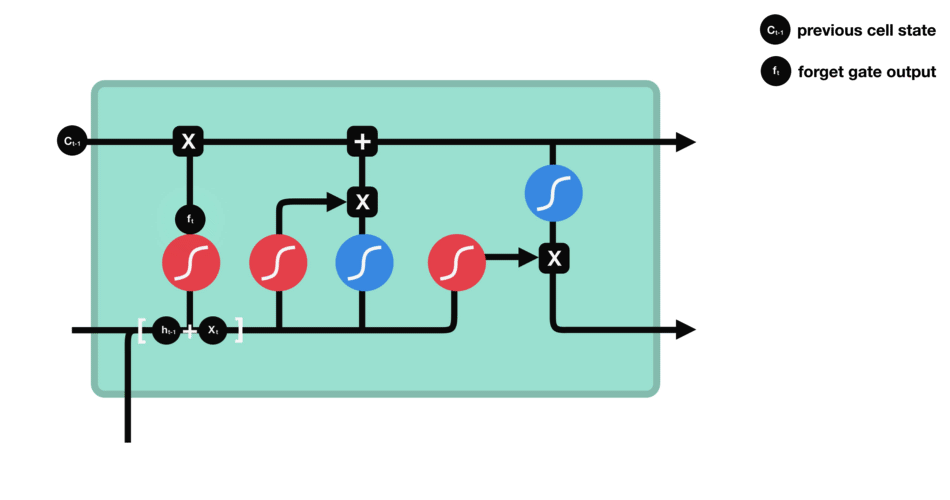
This gate 决定了那些info需要被遗弃,哪些要保留。
- 上一cell的隐状态$h_{t-1}$与本cell的输入$x_t$连在一起
- 经过sigmoid
- 靠近0的被遗忘,靠近1的本保留。
- 得到向量
$f_t$
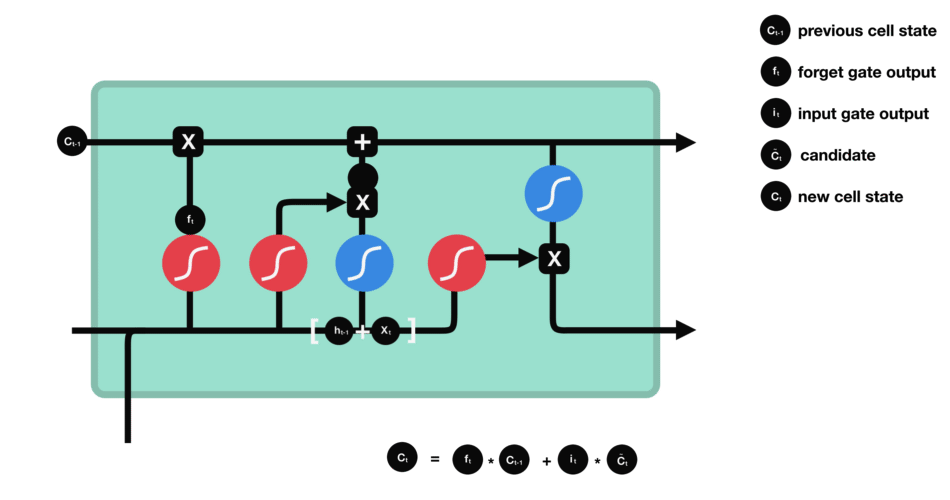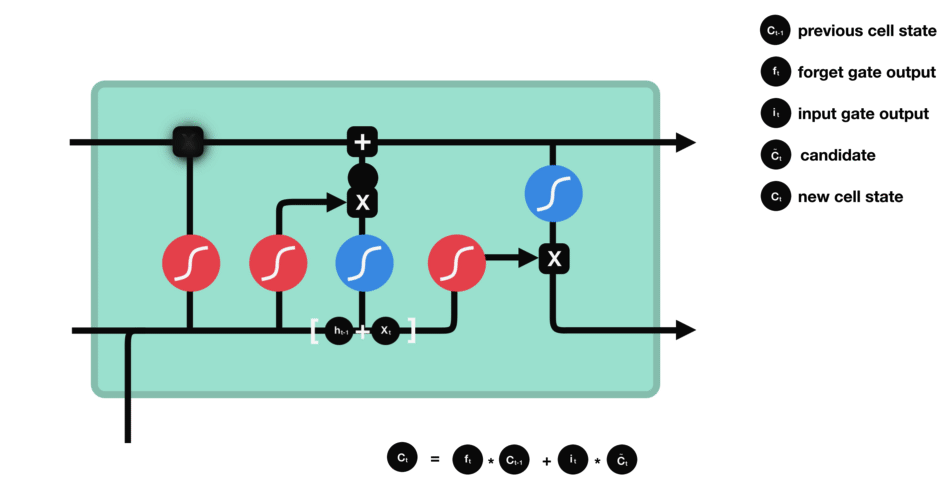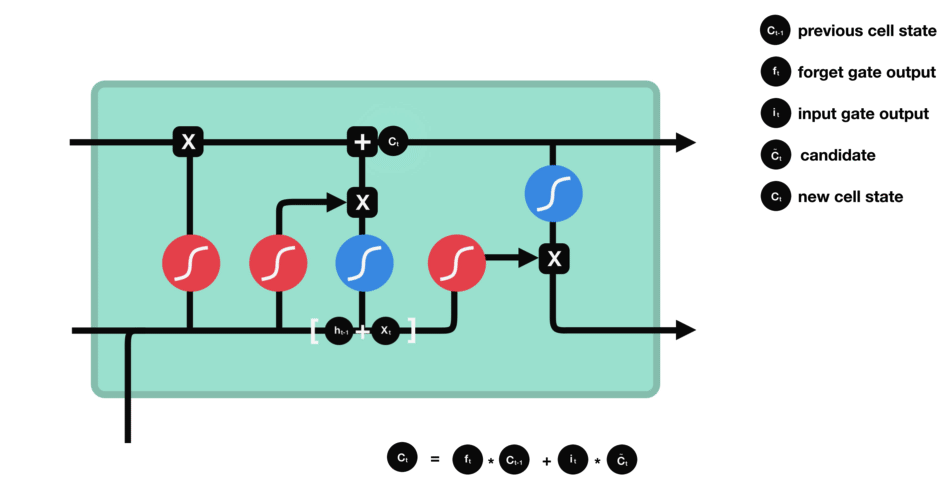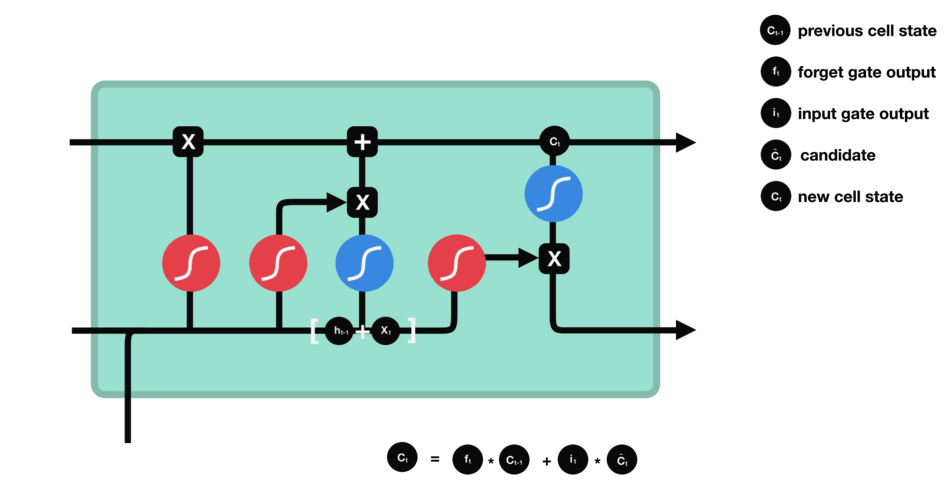
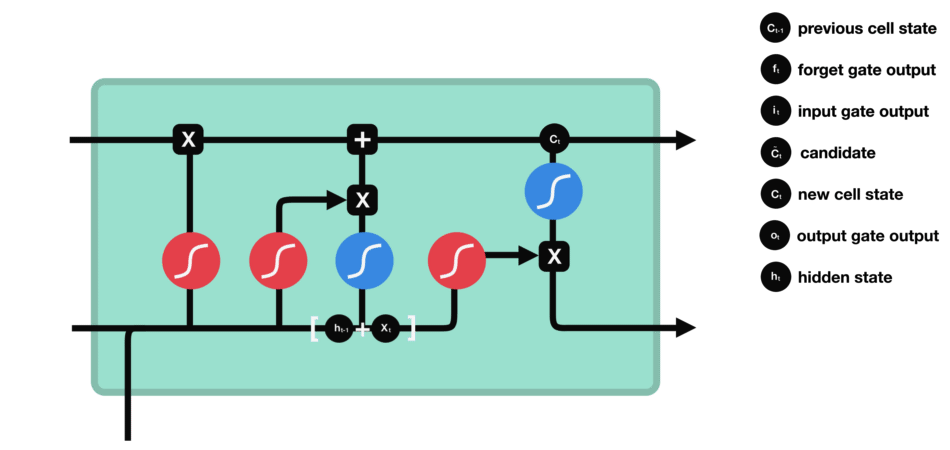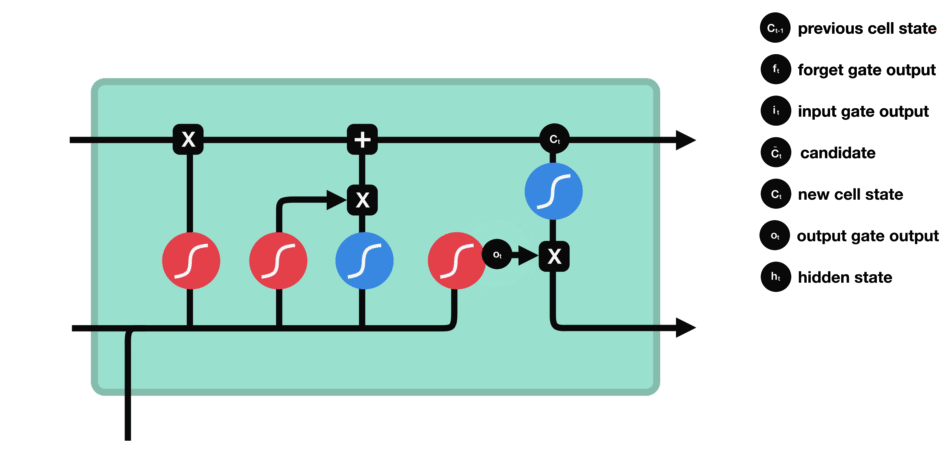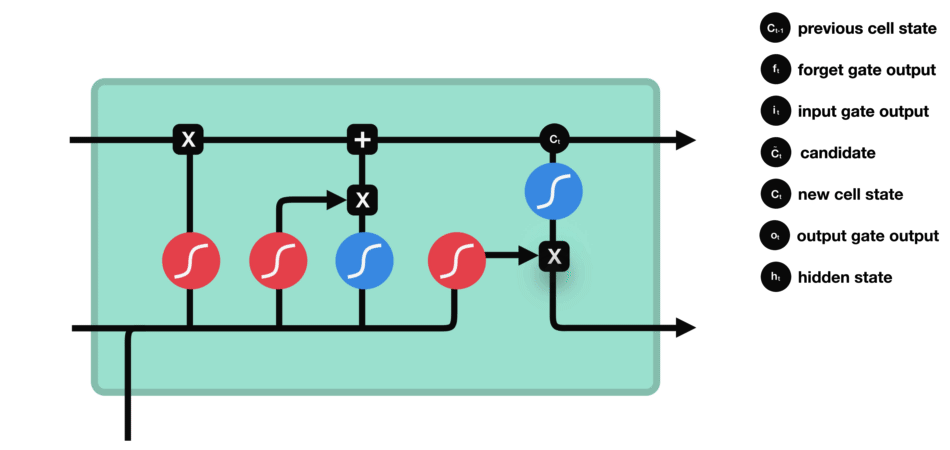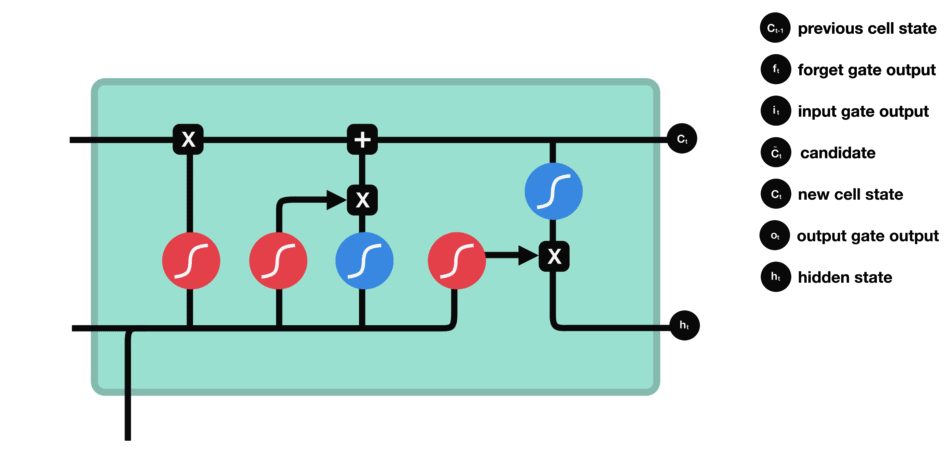
The input gate decides what information is relevant to add from the current step.
-
$h_{t-1}+x_t$ 经过一个sigmoid,来确定要更新那些值,0-1不重要,1表示重要, 即为$i_t$ - 同时,$h_{t-1}+x_t$经过tanh函数,用以将值压缩到(-1,1)区间, 得到
$g_t$ - 将二者的结果乘到一起,sigmoid的输出将决定来保留tanh输出的哪些info
- 上一cell state
$c_{t-1}$ 的乘以遗忘门输出$f_t$ ,部分info被遗弃了 - 加上输入门的输出$i_t\times g_t$ 就得到本cell state
$c_t$
输出门决定了下一个隐状态,这个隐状态是包含过往信息的,同时也被用于预测。
-
$h_{t-1}+x_t$ 经过sigmoid,这和遗忘门的权重参数不一样,得到$o_t$ - cell state经过tanh的范围缩放
- 两者相乘,用以筛选cell state中的重要信息,将其保留在隐状态
$h_t$ 中,既用于下一个cell的计算,也用于当前层的损失估计 $y_t=\sigma(W'h_t)$
我们有必要重新规范地总结一下前向传播公式,即使开头已经提到了:
- 更新遗忘门输出:
$$f_{t}=\sigma\left(W_{f} h_{t-1}+U_{f} x_{t}+b_{f}\right)$$ - 更新输入门两部分输出: $$\begin{array}{c}i_{t}=\sigma\left(W_{i} h_{t-1}+U_{i} x_{t}+b_{i}\right) \g_{t}=\tanh \left(W_{g} h_{t-1}+U_{g} x_{t}+b_{g}\right)\end{array}$$
- 更新细胞状态:
$$C_{t}=C_{t-1} \odot f_{t}+i_{t} \odot g_{t}$$ - 更新输出门输出: $$\begin{array}{c}o_t=\sigma\left(W_{o} h_{t-1}+U_{o} x_t +b_{o}\right) \h_t=o_t \odot \tanh \left(C_t\right)\end{array}$$
- 更新当前cell预测输出:
$$\hat{y}_t=\sigma\left(V h_t+b_y\right)$$
总结一下: $$\text {gate state } s_{t}=\left[\begin{array}{c} g_{t} \ i_{t} \ f_{t} \ o_{t} \end{array}\right], W=\left[\begin{array}{c} W_{g} \ W_{i} \ W_{f} \ W_{o} \end{array}\right], U=\left[\begin{array}{c} U_{g} \ U_{i} \ U_{f} \ U_{o} \end{array}\right], b=\left[\begin{array}{c} b_{g} \ b_{i} \ b_{f} \ b_{o} \end{array}\right]$$
self.H = 128 # Number of LSTM layer's neurons
self.D = 10000 # Number of input dimension == number of items in vocabulary
Z = self.H + self.D # Because we will concatenate LSTM state with the input
self.model = dict(
Wf=np.random.randn(Z, self.H) / np.sqrt(Z / 2.),
Wi=np.random.randn(Z, self.H) / np.sqrt(Z / 2.),
Wc=np.random.randn(Z, self.H) / np.sqrt(Z / 2.),
Wo=np.random.randn(Z, self.H) / np.sqrt(Z / 2.),
Wy=np.random.randn(self.H, self.D) / np.sqrt(self.D / 2.),
bf=np.zeros((1, self.H)),
bi=np.zeros((1, self.H)),
bc=np.zeros((1, self.H)),
bo=np.zeros((1, self.H)),
by=np.zeros((1, self.D))
)
def lstm_forward(self, X, state):
m = self.model
Wf, Wi, Wc, Wo, Wy = m['Wf'], m['Wi'], m['Wc'], m['Wo'], m['Wy']
bf, bi, bc, bo, by = m['bf'], m['bi'], m['bc'], m['bo'], m['by']
h_old, c_old = state
# One-hot encode
X_one_hot = np.zeros(self.D)
X_one_hot[X] = 1.
X_one_hot = X_one_hot.reshape(1, -1)
# Concatenate old state with current input
X = np.column_stack((h_old, X_one_hot))
hf = sigmoid(X @ Wf + bf)
hi = sigmoid(X @ Wi + bi)
ho = sigmoid(X @ Wo + bo)
hc = tanh(X @ Wc + bc)
c = hf * c_old + hi * hc
h = ho * tanh(c)
y = h @ Wy + by
prob = softmax(y)
state = (h, c) # Cache the states of current h & c for next iter
cache = (hf, hi, ho, hc, c, h, y, Wf, Wi, Wc, Wo, Wy, X, c_old) # Add all intermediate variables to this cache
return prob, state, cache
记住这些参数:
- 遗忘门状态
$f_t$ , 输入门状态$i_t$ , 当前cell新输入信息$g_t$ , 当前cell状态$C_t$ , 输出门状态$o_t$ , 当前cell隐状态$h_t$ , 模型输出$y_t$
对于LSTM的反向传播,我们需要从cell state
为方便计算,把Loss写作递归形式,用以展示时序之间的影响,$\tau$是最后序列索引位置:
-
最后序列索引位置处 $$\begin{array}{c}\delta_{h}^{(\tau)}=\left(\frac{\partial o_{\tau}}{\partial h_{\tau}}\right)^{T} \frac{\partial L_{\tau}}{\partial o_{\tau}}=V^{T}\left(\hat{y}{\tau}-y{\tau}\right) \\delta_{C}^{(\tau)}=\left(\frac{\partial h_{\tau}}{\partial C_{\tau}}\right)^{T} \frac{\partial L_{\tau}}{\partial h_{\tau}}=\delta_{h}^{(\tau)} \odot o_{\tau} \odot\left(1-\tanh ^{2}\left(C_{\tau}\right)\right)\end{array}$$
-
以
$\delta_{C}^{(t+1)}, \delta_{h}^{(t+1)}$ 反推$\delta_{C}^{(t)}, \delta_{h}^{(t)}$ :-
$\delta_{h}^{(t)}$ : $$\begin{aligned} \delta_{h}^{(t)}&=\frac{\partial L}{\partial h_{t}}\&=\frac{\partial l(t)}{\partial h_{t}}+\left(\frac{\partial h_{t+1}}{\partial h_{t}}\right)^{T} \frac{\partial L(t+1)}{\partial h_{t+1}}\&=V^{T}\left(\hat{y}{t}-y{t}\right)+\left(\frac{\partial h_{t+1}}{\partial h_{t}}\right)^{T} \delta_{h}^{t+1} \end{aligned}$$ 整个LSTM反向传播的难点就在于$\frac{\partial h_{t+1}}{\partial h_t}$ 这部分的计算。我们知道,$h_{t+1}=o_{t+1} \odot \tanh \left(C_{t+1}\right)$。
-
$o_{t+1}=\sigma\left(W_{o} h_{t}+U_{o} x_{t+1} +b_{o}\right)$ 包含了$h_{t}$。 -
$C_{t+1}=C_{t} \odot f_{t+1}+i_{t+1} \odot g_{t+1}$ ,其中$f_{t+1}, i_{t+1}, g_{t+1}$ 分别包含了$h_{t}$。$f_{t+1}=\sigma\left(W_{f} h_{t}+U_{f} x_{t+1}+b_{f}\right)$ $i_{t+1}=\sigma\left(W_{i} h_{t}+U_{i} x_{t+1}+b_{i}\right)$ -
$g_{t+1}=\tanh \left(W_{g} h_{t}+U_{g} x_{t+1}+b_{g}\right)$ 那么$\delta_{h}^{(t)}$ 的计算就分为以下四部分: $$\begin{aligned}\frac{\partial h_{t+1}}{\partial h_t}&= \left[o_{t+1} \odot\left(1-o_{t+1}\right) \odot \tanh \left(C_{t+1}\right)\right] W_{o} \&\quad+ \left[\Delta C \odot f_{t+1} \odot\left(1-f_{t+1}\right) \odot C_{t}\right] W_{f} \&\quad+ \left{\Delta C \odot i_{t+1} \odot\left[1-\left(a_{t+1}\right)^{2}\right]\right} W_{a} \&\quad+ \left[\Delta C \odot a_{t+1} \odot i_{t+1} \odot\left(1-i_{t+1}\right)\right] W_{i}\end{aligned}$$ 其中:$$\Delta C=o_{t+1} \odot\left[1-\tanh ^{2}\left(C_{t+1}\right)\right]$$
-
-
$\delta_{C}^{(t)}$ : $$\begin{aligned}\delta_{C}^{(t)}&=\left(\frac{\partial C_{t+1}}{\partial C_{t}}\right)^{T} \frac{\partial L}{\partial C_{t+1}}+\left(\frac{\partial h_{t}}{\partial C_{t}}\right)^{T} \frac{\partial L}{\partial h_{t}}\&=\left(\frac{\partial C_{t+1}}{\partial C_{t}}\right)^{T} \delta_{C}^{(t+1)}+\delta_{h}^{(t)} \odot o_{t}\odot\left(1-\tanh ^{2}\left(C_{t}\right)\right)\&=\delta_{C}^{(t+1)} \odot f_{t+1}+\delta_{h}^{(t)} \odot o_{t} \odot\left(1-\tanh ^{2}\left(C_{t}\right)\right)\end{aligned}$$
-
-
计算出上面两个偏导后,剩下的就容易了,以
$W_f$ 为例:$$\frac{\partial L}{\partial W_{c}}=\sum^{\tau}\left[\delta_{C}^{(t)} \odot C_{t-1} \odot f_{t} \odot\left(1-f_{t}\right)\right]\left(h_{t-1}\right)^{T}$$
def lstm_backward(self, prob, y_train, d_next, cache):
# Unpack the cache variable to get the intermediate variables used in forward step
hf, hi, ho, hc, c, h, y, Wf, Wi, Wc, Wo, Wy, X, c_old = cache
dh_next, dc_next = d_next
# Softmax loss gradient
dy = prob.copy()
dy -= y_train
dy = sigmoid_derivative(dy)
# Hidden to output gradient
dWy = h.T @ dy
dby = dy
# Note we're adding dh_next here
dh = dy @ Wy.T + dh_next
# Gradient for ho in h = ho * tanh(c)
dho = tanh(c) * dh
dho = sigmoid_derivative(ho) * dho
# Gradient for c in h = ho * tanh(c), note we're adding dc_next here
dc = ho * dh * tanh_derivative(c)
dc = dc + dc_next
# Gradient for hf in c = hf * c_old + hi * hc
dhf = c_old * dc
dhf = sigmoid_derivative(hf) * dhf
# Gradient for hi in c = hf * c_old + hi * hc
dhi = hc * dc
dhi = sigmoid_derivative(hi) * dhi
# Gradient for hc in c = hf * c_old + hi * hc
dhc = hi * dc
dhc = tanh_derivative(hc) * dhc
# Gate gradients, just a normal fully connected layer gradient
dWf = X.T @ dhf
dbf = dhf
dXf = dhf @ Wf.T
dWi = X.T @ dhi
dbi = dhi
dXi = dhi @ Wi.T
dWo = X.T @ dho
dbo = dho
dXo = dho @ Wo.T
dWc = X.T @ dhc
dbc = dhc
dXc = dhc @ Wc.T
# As X was used in multiple gates, the gradient must be accumulated here
dX = dXo + dXc + dXi + dXf
# Split the concatenated X, so that we get our gradient of h_old
dh_next = dX[:, :self.H]
# Gradient for c_old in c = hf * c_old + hi * hc
dc_next = hf * dc
grad = dict(Wf=dWf, Wi=dWi, Wc=dWc, Wo=dWo, Wy=dWy, bf=dbf, bi=dbi, bc=dbc, bo=dbo, by=dby)
state = (dh_next, dc_next)
return grad, state
- Keras RNN
- Keras LSTM tutorial – How to easily build a powerful deep learning language model
- Illustrated Guide to LSTM’s and GRU’s: A step by step explanation
- Understanding LSTM Networks
- LSTM Neural Network from Scratch Kaggle
- LSTM结构理解与python实现
- 详细阐述基于时间的反向传播算法(Back-Propagation Through Time,BPTT)
- Deriving LSTM Gradient for Backpropagation
- Deriving the gradients for Backward propagation in LSTM