Classification & Regression
树结构是算法中常见的数据结构,主要元素如下:
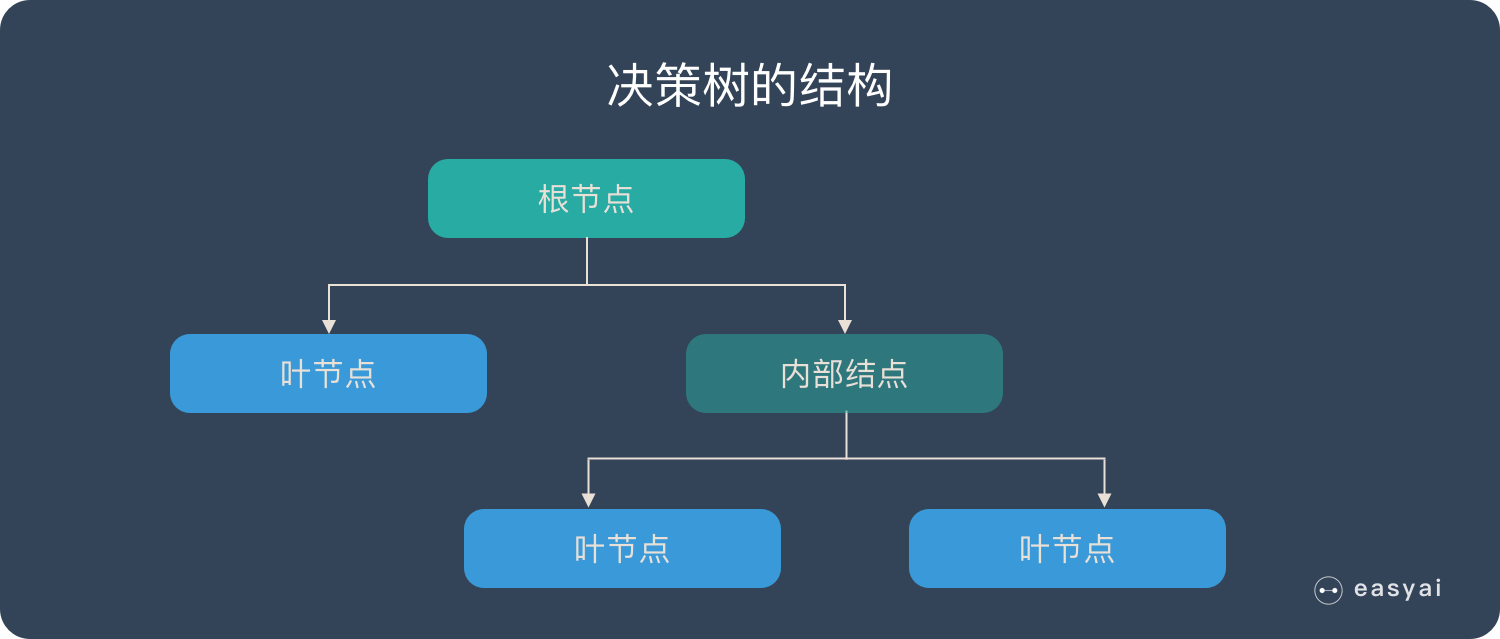
- 根节点:包含样本的全集
- 内部节点:对应特征属性测试
- 叶节点:代表决策的结果
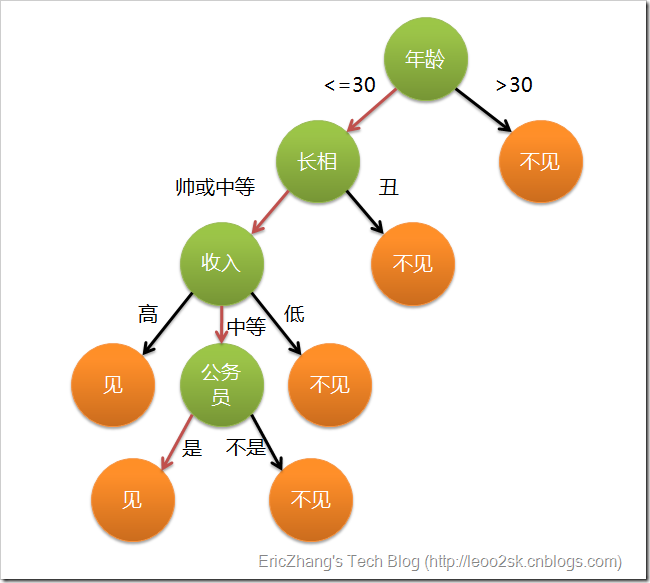
以相亲为例
摘自 算法杂货铺——分类算法之决策树(Decision tree)
至于其中内部节点和叶节点对应的具体参数,就需要我们通过训练得到,因此是一种基于 if-then-else 规则的有监督学习算法,也可以理解为函数的离散逼近方法。
- 特征选择:筛选出跟分类结果相关性较高的特征,也就是分类能力较强的特征。在特征选择中通常使用的准则是:信息增益;
小姐姐从备胎里挑男朋友的时候,肯定要有个判定标准噻!要是认为颜值最重要,那肯定先用颜值刷掉一批人;要是身高控,可能就先从身高筛。筛的顺序还得看小姐姐口味(根据具体问题再具体讨论)。
- 决策树生成:选择好特征后,就从根节点触发,对节点计算所有特征的信息增益,选择信息增益最大的特征作为节点特征,根据该特征的不同取值建立子节点;对每个子节点使用相同的方式生成新的子节点,直到信息增益很小或者没有特征可以选择为止。
小姐姐把自己的标准整理了一下,形成了一个套成熟的备胎上位评判体系。
- 决策树剪枝:对抗「过拟合」。
后来,小姐姐发现自己要求太多了,筛起来太累,就删了几条无关痛痒的标准:戴不戴眼镜、穿不穿AJ (误?)
- ID3: 只可用于离散特征。应用信息增益来选择特征;
- C4.5: ID3改进版,离散+连续。引入“信息增益率”指标作为特征的选择依据;
- CART: 即可分类又可回归。使用了基尼系数取代了信息熵模型。
设D为用类别对训练元组进行的划分,则D的熵(entropy)表示为: $$i n f o(D)=-\sum_{i=1}^{m} p_{i} \log {2}\left(p{i}\right)$$
其中pi表示第i个类别在整个训练元组中出现的概率,可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中信息的不确定程度,熵越大越不确定。如下图,熵最大时,概率为0.5,正是一无所知的位置。
现在我们假设将训练元组D按属性A进行划分,则A对D划分的期望信息为:
信息增益即为两者的差值:
意味着增加节点后,系统熵减的程度。
以上没看懂的这里集合,全网最简单的理解在这里!
一个颜控小姐姐且不物质的小姐姐,初筛看money的话会剩下很多备胎,但是初筛看颜值的话可能就一步到位了!对她来说,颜值就是系统熵减最大的特征,让她能够在一次筛选中,最大程度地缩小范围(降低信息不确定性)。
ID3出什么问题了,我们为什么要改进?
凡事勿过度 --德尔斐神谕
信息增益的计算依赖于特征数目较多的特征,而属性取值最多的属性并不一定最优。非递增算法。单变量决策树。
如果出现一个特征,是备胎的名字,这毋庸置疑是熵减最大的,真实的一步到位!(除非小姐姐会玩,有两个备胎:Mike A、Mike B,还能分清楚)这肯定不算是建立评判体系啦!
$$i n f o_{A}(D)=\sum_{i=1} \frac{1}{n} \log _{2}(1)=0$$
定义:分裂信息
$$split_info_{A}(D)=-\sum_{j=1}^{v} \frac{\left|D_{j}\right|}{|D|} \log {2}\left(\frac{\left|D{j}\right|}{|D|}\right)$$
信息增益率:
继续集合!
既然分的份数影响了我们分裂,那就把它考虑进去做个罚项嘛,那就做分母好了。这就是分裂信息。
Gini如果为0,说明集合纯净,Gini大则说明集合离散度高。所以我们选择,使Gini系数最小的feature来生成枝叶:
看到纯净别怕,其实和熵一样,就是信息不确定度。只是省去了log计算。
CART又被称作分类回归树 回归时不就是二分法?详见:决策树算法原理(下)
优点:
- 简单直观
- 基本不需要数据预处理,归一化,处理缺失值
- 预测代价O(logm),m为样本数
- 适用于离散和连续数据
- 逻辑上可以较好的解释,相较于神经网络的黑盒
- 可以用交叉验证的剪枝来提高泛化能力
- 对异常点容错能力好
缺点:
- 非常容易过拟合。可以通过设置节点样本数量和先知决策树深度以及后剪枝来改进
- 树的结构会因为样本的一点点改动而剧烈改变。可以通过集成学习方法改进
- 因为是贪心算法,只能确定局部最优。通过集成学习改进
- 如果某特征样本比例过大,生成的决策树容易偏向这些特征,造成欠拟合。可以通过调节样本权重来改进。