You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
I used the ten_armed_testbed.py to solve excercise 2.5, but the result shows that sample-average method outperforms constant step-size method(I set alpha=0.1) in the non-stationary problems, which is contrary to the book:
Note that both convergence conditions are met for the sample-average case, n(a) = 1/n, but not for the case of constant step-size parameter. In the latter case, the second condition is not met, indicating that the estimates never completely converge but continue to vary in response to the most recently received rewards. As we mentioned above, this is actually desirable in a nonstationary environment, and problems that are effectively nonstationary are the most common in reinforcement learning.
here's a result of mine:
when I add a random number follows the standard normal distribution to the reward and set the time to 10000 for every episode:
here's my code:
######################################################################## Copyright (C) ## 2016-2018 Shangtong Zhang([email protected]) ## 2016 Tian Jun([email protected]) ## 2016 Artem Oboturov([email protected]) ## 2016 Kenta Shimada([email protected]) ## Permission given to modify the code as long as you keep this ## declaration at the top ########################################################################importmatplotlibimportmatplotlib.pyplotaspltimportnumpyasnpfromtqdmimporttrangematplotlib.use('Agg')
classBandit:
# @k_arm: # of arms# @epsilon: probability for exploration in epsilon-greedy algorithm# @initial: initial estimation for each action# @step_size: constant step size for updating estimations# @sample_averages: if True, use sample averages to update estimations instead of constant step size# @UCB_param: if not None, use UCB algorithm to select action# @gradient: if True, use gradient based bandit algorithm# @gradient_baseline: if True, use average reward as baseline for gradient based bandit algorithmdef__init__(self, k_arm=10, epsilon=0., initial=0., step_size=0.1, sample_averages=False, UCB_param=None,
gradient=False, gradient_baseline=False, true_reward=0.):
self.k=k_armself.step_size=step_sizeself.sample_averages=sample_averagesself.indices=np.arange(self.k)
self.time=0self.UCB_param=UCB_paramself.gradient=gradientself.gradient_baseline=gradient_baselineself.average_reward=0self.true_reward=true_rewardself.epsilon=epsilonself.initial=initialdefreset(self):
# real reward for each actionself.q_true=np.random.randn(self.k) +self.true_reward# estimation for each actionself.q_estimation=np.zeros(self.k) +self.initial# # of chosen times for each actionself.action_count=np.zeros(self.k)
self.best_action=np.argmax(self.q_true)
self.time=0# get an action for this banditdefact(self):
ifnp.random.rand() <self.epsilon:
returnnp.random.choice(self.indices)
ifself.UCB_paramisnotNone:
UCB_estimation=self.q_estimation+ \
self.UCB_param*np.sqrt(np.log(self.time+1) / (self.action_count+1e-5))
q_best=np.max(UCB_estimation)
returnnp.random.choice(np.where(UCB_estimation==q_best)[0])
ifself.gradient:
exp_est=np.exp(self.q_estimation)
self.action_prob=exp_est/np.sum(exp_est)
returnnp.random.choice(self.indices, p=self.action_prob)
q_best=np.max(self.q_estimation)
returnnp.random.choice(np.where(self.q_estimation==q_best)[0])
# take an action, update estimation for this actiondefstep(self, action):
# generate the reward under N(real reward, 1)reward=np.random.normal() +self.q_true[action] # nonstationary self.time+=1self.action_count[action] +=1self.average_reward+= (reward-self.average_reward) /self.timeifself.sample_averages:
# update estimation using sample averagesself.q_estimation[action] += (reward-self.q_estimation[action]) /self.action_count[action]
elifself.gradient:
one_hot=np.zeros(self.k)
one_hot[action] =1ifself.gradient_baseline:
baseline=self.average_rewardelse:
baseline=0self.q_estimation+=self.step_size* (reward-baseline) * (one_hot-self.action_prob)
else:
# update estimation with constant step sizeself.q_estimation[action] +=self.step_size* (reward-self.q_estimation[action])
returnrewarddefsimulate(runs, time, bandits):
rewards=np.zeros((len(bandits), runs, time))
best_action_counts=np.zeros(rewards.shape)
fori, banditinenumerate(bandits):
forrintrange(runs):
bandit.reset()
fortinrange(time):
action=bandit.act()
reward=bandit.step(action)
rewards[i, r, t] =rewardifaction==bandit.best_action:
best_action_counts[i, r, t] =1mean_best_action_counts=best_action_counts.mean(axis=1)
mean_rewards=rewards.mean(axis=1)
returnmean_best_action_counts, mean_rewardsdeffigure(runs=2000, time=10000):
eps=0.1bandits= [Bandit(epsilon=eps, sample_averages=True) ,Bandit(epsilon=eps, sample_averages=False,step_size=0.1)]
best_action_counts, rewards=simulate(runs, time, bandits)
plt.figure(figsize=(10, 20))
plt.subplot(2, 1, 1)
formethod, rewardsinzip(('sample averages','constant step-size'), rewards):
plt.plot(rewards, label=method)
plt.xlabel('steps')
plt.ylabel('average reward')
plt.legend()
plt.subplot(2, 1, 2)
formethod, countsinzip(('sample averages','constant step-size'), best_action_counts):
plt.plot(counts, label=method)
plt.xlabel('steps')
plt.ylabel('% optimal action')
plt.legend()
plt.savefig('../images/figure_2_7_5.png')
plt.close()
if__name__=='__main__':
figure()
Why is this happening ? Shouldn't the constant step-size method has higher reward in the long run in the non-stationary condition?Or I made some mistakes in coding? Hope someone can help me with this.
The text was updated successfully, but these errors were encountered:
I used the
ten_armed_testbed.pyto solve excercise 2.5, but the result shows that sample-average method outperforms constant step-size method(I set alpha=0.1) in the non-stationary problems, which is contrary to the book:here's a result of mine:
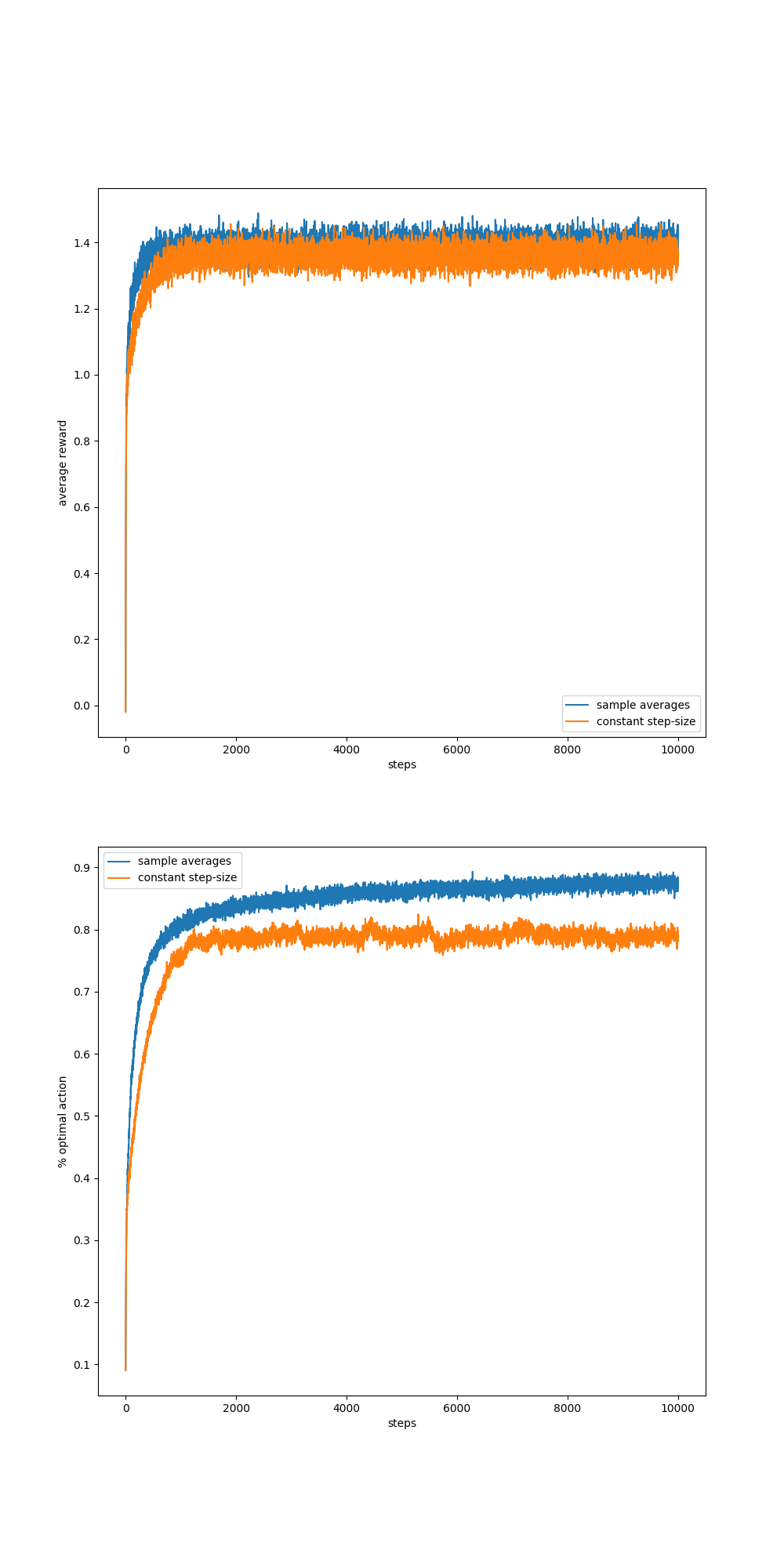
when I add a random number follows the standard normal distribution to the reward and set the time to 10000 for every episode:
here's my code:
Why is this happening ? Shouldn't the constant step-size method has higher reward in the long run in the non-stationary condition?Or I made some mistakes in coding? Hope someone can help me with this.
The text was updated successfully, but these errors were encountered: