#WordNet
##Summary: This assignment take two input files to build a wordnet DAG, aftering building the graph, we can find the relation between two words.
###Input files:
-
List of synsets. This contains all noun synsets in WordNet, one per line. Line i of the file (counting from 0) contains the information for synset i. The first field is the synset id, which is always the integer i; the second field is the synonym set (or synset); and the third field is its dictionary definition (or gloss), which is not relevant to this assignment.
-
List of hypernyms. The file hypernyms.txt contains the hypernym relationships. Line i of the file (counting from 0) contains the hypernyms of synset i. The first field is the synset id, which is always the integer i; subsequent fields are the id numbers of the synset's hypernyms.
-
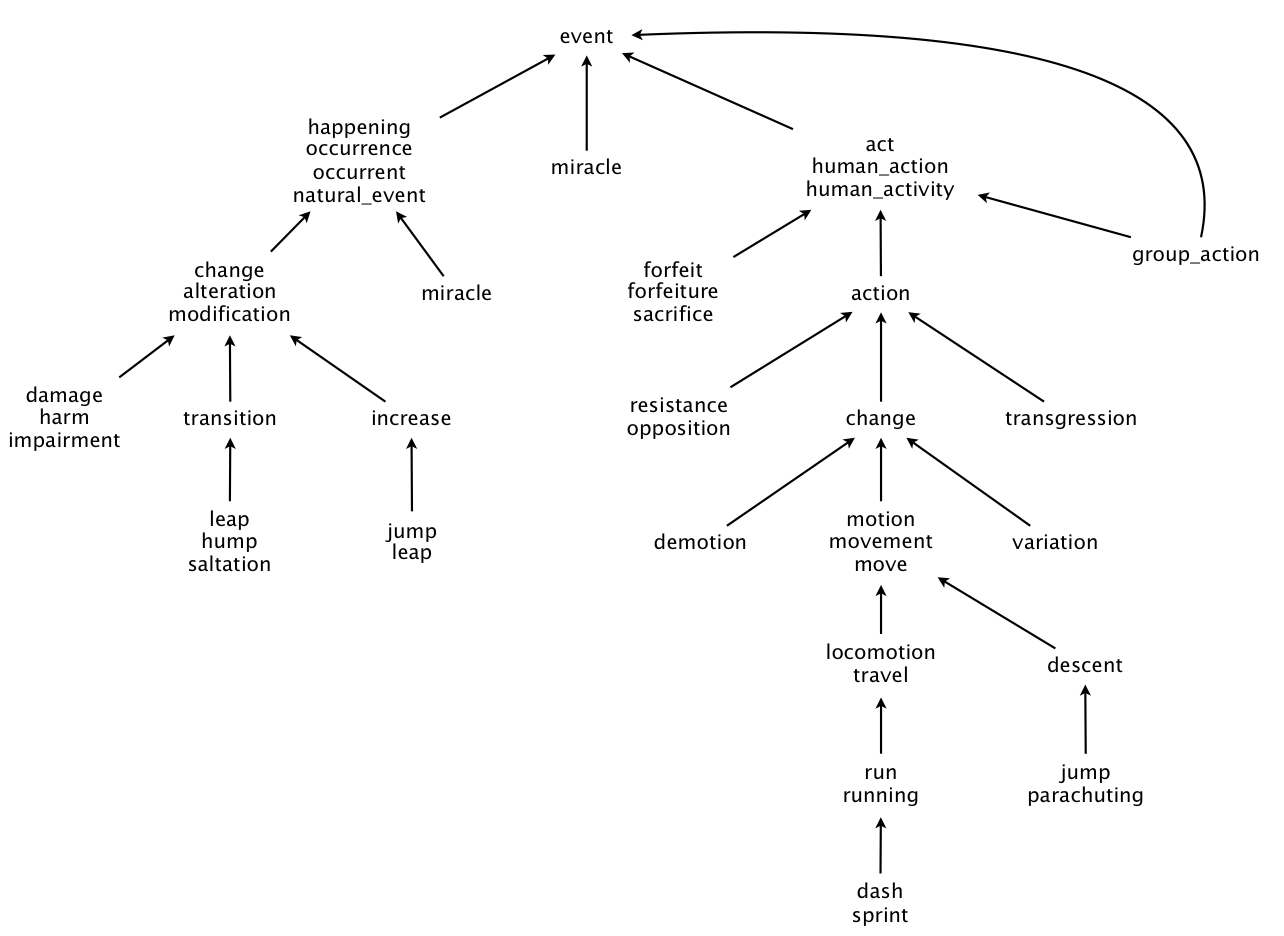
Note:A hyponym(more specific synset) might point to multiple hypernyms(more general sets), take a look on the graph below.
###Classes:
-
WordNet : This is the main body of the application, we take the input synsets.txt and hypernym.txt to build a graph and initialize a SAP instance which will be use to compute the length and ancestor between two word.
-
SAP : This is the object to sovle the shortest distance and the shortest common ancestor between two points, we initialize this intance with a DAG, then the job is to take two int and calculate.
-
Outcast : This object can find the least related word in a file compare to other words, which means, to find out the word with largest sum of legth to other words.
##Reviews: WordNet : Input file synsets.txt maps words to its id, hypernyms maps ids to its parent ids. To build the complete wordnet, we have to build a hashmap to map each noun to its id sets, which is for the mapping between the input nouns and the graph ids. Moreover, we have to buil id maps between children id and parent id, this tells us a specific set belongs to which general set. This is the fundation for constructing the graph.
SAP : This is the main solution of the problem, it is a very classical Breadth-First Search. Instead of using the provided class, i decided to implement the algorithm on my own, which eventually saved me lots of time and tons of memory. This is a solution both memory and time-efficient.
| Test | WordNet Constructor | Length&Ancestor Calculation Calls | isNoun calls |
|---|---|---|---|
| Benchmark | 0.81 seconds | 218282.80 | 601080.00 |
| My Solution | 10.00 seconds | 127528.00 | 434408.00 |
| Ratio | 1.71 | 1.38 |
The only thing i need to mention is the problem i met while implementing the BFS algorithm. Since the input may contain a self-cycle point, and i used a queue to keep a list of vertex that are going to be visited and a set of vertex that have already been visted along with the depth they were, there could be a situation, for example, i enqueued 0 and put its id and depth into the set, at the same time 0 is self-cycled, so this vertex will be examined and add to the SET again with its depth incremented 1, this will give us the wrong results. So we have to add a if statement to rule out this scenario. See codes below:
while (!queue1.isEmpty()) {
int size = queue1.size();
for (int i = 0; i < size; i++) {
int id = queue1.dequeue();
for (int v : G.adj(id)) {
if (visited1.contains(Integer.valueOf(v))) {
continue;
}
queue1.enqueue(Integer.valueOf(v));
}
// since we only check the set instead of the queue, so a point might enter the queue twice if it was a self-cycle point this will cause the length to increment by one
if (visited1.contains(Integer.valueOf(id))) {
int existLength = visited1.get(Integer.valueOf(id));
if (existLength < depth1) {
continue;
}
}
visited1.put(Integer.valueOf(id), Integer.valueOf(depth1));
}
depth1++;
}
0---->1 | ^ |__2__|
As shown in the graph above, the length between 0 and 1 is 1, however, if we dont have the snippet above, we will enqueue 2 and 1 at the first time, and during the second loop, if we dequeue 2 first, we will enqueue its neighbor 1 into the queue again. As we can see from the graph, after dequeue the first 1 in the queue, we will have length 1 for Integer 1. However, if we process the one again, we will increment the length of 1 to two, whivh will leads to the wrong result.
Outcast : Just iterate each noun and calculate the sum of distance between the noun and others, pick the noun with the max sum.